Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

định lý thường nói : nếu trong 1 tam giác có tông độ dài hai cạnh luôn luôn lớn hơn cạnh còn lại
bạn dựa vào định lý đó để chứng minh
thanks

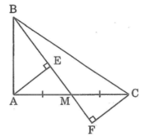
Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .

a: Xét ΔMEA vuông tại E và ΔMFC vuông tại F có
MA=MC
góc AME=góc CMF
=>ΔMEA=ΔMFC
=>ME=MF
b: BE+BF
=BE+BE+EF
=BE+BE+2*ME
=2*BE+2*ME
=2*BM
c: ΔAMB vuông tại A
=>AB<BM

chín phần hai mươi đề xi mét khối băng bao nhiêu xăng ti mét khối
Vì sao?

a: Xét ΔAME vuông tại E và ΔCMF vuông tại F có
MA=MC
góc AME=góc CMF
=>ΔAME=ΔCMF
b: BE+BF=2BE+EF
=2BE+2ME
=2BM>2BA
=>AB<(BE+BF)/2
khong biet nha ban