Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Do đó: ADME là hình chữ nhật

b: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật

b: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật

a)\(\Delta ABC\) vuông tại A nên \(\widehat{BAC}=90^o\Rightarrow\widehat{DAE}=90^o\)
Có D là hình chiếu của M trên AB \(\Rightarrow MD\perp AB\Rightarrow\widehat{MDA}=90^o\)
Có E là hình chiếu của M trên AC \(\Rightarrow ME\perp AC\Rightarrow\widehat{AEM}=90^o\)
Xét tứ giác: \(ADEM\) có \(\left\{{}\begin{matrix}\widehat{DAE}=90^o\\\widehat{MDA}=90^o\\\widehat{AEM}=90^o\end{matrix}\right.\)
\(\Rightarrow\)Tứ giác ADEM là hình chữ nhật
Vậy tứ giác ADEM là hình chữ nhật.
b)\(\Delta ABC\) vuông tại A có AM là trung tuyến (M là trung điểm BC)
\(\Rightarrow AM=\dfrac{1}{2}BC\)
Mà \(AM=DE\) (tính chất hcn)
\(\Rightarrow DE=\dfrac{1}{2}BC\left(đpcm\right)\)
Bổ sung đề: Tam giác ABC vuông tại A
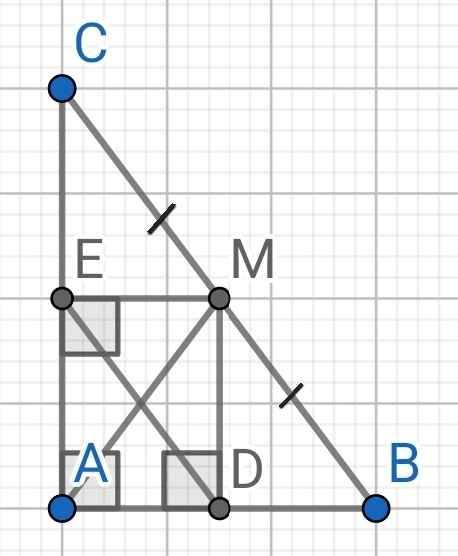 a) Xét tứ giác ADME có:
a) Xét tứ giác ADME có:
∠AEM = ∠EAD = ∠ADM = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do ADME là hình chữ nhật (cmt)
⇒ AM = DE (1)
Lại có:
AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BC/2 (2)
Từ (1) và (2) ⇒ DE = BC/2

Do MD\(\perp\)AB tại D =)\(\widehat{A\text{D}M}\)=900
Do ME\(\perp\)AC tại E =)\(\widehat{A\text{E}M}\)=900
Do tam giác ABC vuông tại A =) \(\widehat{BAC}\)=900
Xét tứ giác ADME có:
\(\widehat{A\text{D}M}\)=\(\widehat{A\text{E}M}\)=\(\widehat{BAC}\) ( vì cùng bằng 900)
=) ADME là hình chữ nhật
Xét tam giác ABC có :
M là trung điểm của BC
MD // AC
=) D là trung điểm của AB
Xét tam giác ABC có :
M là trung điểm của BC
ME // AB
=) E là trung điểm của AC
Xét tam giác ABC có :
D là trung điểm của AB
E là trung điểm của AC
=) DE là đường trung bình của tam giác ABC
=) DE //BC =) DE //BM (1)
Và DE= \(\frac{BC}{2}\)=BM=CM (vì M là trung điểm của BC ) (2)
Từ (1) và (2) =) BDEM là hình bình hành

a: Xét ΔCAB có
N là trung điểm của AB
NP//AB
=>P là trung điểm của AC
Xét ΔCAB có
N là trung điểm của BC
NM//AC
=>M là trung điểm của AB
b: Xét tứ giác ANCE có
P là trung điểm chung của AC và NE
AC vuông góc NE
=>ANCE là hình thoi

Bài 2 :
A B C D M E
a, Xét tam giác ABC ta có :
D là trung điểm AB
M là trung điểm CB
=)) DM là đường TB tam giác ABC
=)) DM // AC hay DM // AE (1)
Ta có : E là trung điểm AC
M là trung điểm BA
=)) EM là đường TB tam giác ABC
=)) EM // AB hay EM // AD (2)
Từ 1;2 =)) Tứ giác ADME là hình bình hành
b, Nếu tam giác ABC cân tại A => AM là đường trung tuyến AM
=)) AM đồng thời là tia phân giác của ^A
Xét hình bình hành ADME có 2 đường chéo AM là tia phân giác của ^A (cmt)
=)) Tứ giác ADME là hình thoi
c, Nếu tam giác ABC vuông tại A => ^A = 90^0
Xét hình bình hành ADME có ^A =90^0
=)) Tứ giác ADME là hình chữ nhật
Ta có D, E là hình chiếu của M trên AB, AC
=> DM ⊥ AB và ME ⊥ AC Mà AB ⊥ AC
=> ADME là hình chữ nhật