

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a)\(\widehat{C}=\widehat{BAH}=90^O-\widehat{CAH}\)
\(\widehat{B}=\widehat{CAH}=90^O-\widehat{BAH}\)
b)Ta có:
\(\widehat{ADC}=\widehat{B}+\widehat{BAD}=\widehat{B}+\frac{\widehat{BAH}}{2}=\widehat{B}+\widehat{\frac{C}{2}}\)
Lại có:
\(\widehat{DAC}=180^O-\widehat{C}-\widehat{ADC}=180^O-\widehat{C}-\left(\widehat{B}+\widehat{\frac{C}{2}}\right)=\left(90^O-\widehat{B}\right)-\frac{\widehat{C}}{2}+\left(90^O-\widehat{C}\right)\)
\(=\widehat{C}-\widehat{\frac{C}{2}}+\widehat{B}=\widehat{B}+\frac{\widehat{C}}{2}\)
Suy ra:\(\widehat{ADC}=\widehat{DAC}\)
\(\Rightarrow\Delta ADC\)cân tại C
c)\(DK\perp BC;AH\perp BC\Rightarrow DK//AH\)
\(\Rightarrow\widehat{KDA}=\widehat{DAH}\)(hai góc so le trong)
Mà \(\widehat{BAD}=\widehat{DAH}\)
\(\Rightarrow\widehat{BAD}=\widehat{KDA}\)
\(\Rightarrow\)\(\Delta KAD\)cân tại K
d)Xét \(\Delta CDK-\Delta CAK\)
\(\hept{\begin{cases}CD=CA\\KD=KA\\CA.chung\end{cases}}\)
\(\Rightarrow\Delta CDK=\Delta CAK\left(c.c.c\right)\)
\(\Rightarrowđpcm\)
e)Xét\(\Delta AID-\Delta AHD\)
\(\hept{\begin{cases}AI=AH\\AD.chung\\\widehat{DAI}=\widehat{DAH}\end{cases}}\)
\(\Rightarrow\widehat{AID}=\widehat{AHD}=90^O\)
\(\Rightarrow DI\perp AB.Mà.AC\perp AB\)
\(\Rightarrow DI//AC\)

a, góc BAH = góc HCA vì cùng phụ vời góc HAC
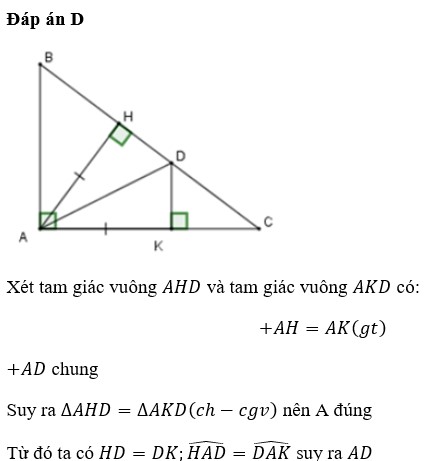
b, Kẻ DK vuông góc với AC.
BA= BD(gt) nên tam giác ABD cân tại A
Suy ra: góc BAD= góc BDA
Mà góc BDA +góc HAD = 90 độ (vì tam giác AHD vuông tại A) ,góc BAD+ góc KAD =góc BAC =90 độ
Do đó: góc HAD =góc KAD
Chứng minh được tam giác HAD =tam giác KAD (cạnh huyền-góc nhọn)
Dẫn đến góc HAD =góc KAD hay góc HAD= góc DAC và lại có tia AD nằm giữa 2 tia AH,AC
Vậy AK là tia p/g của góc HAC
c, tam giác HAD= tam giác KAD(cmt) nên AH=AK
DH=DK (1)
tam giác DKC vuông tại K nên DK<DC (2) và KC<DC
TỪ (1) và (2) suy ra: DH<DC
d, Ta có: AB =BD(gt), AK =AH(cmt) và KC<DC(cmt)
Do đó: AB +AK +KC < BD +AH +DC
Nên : AB+AC < BC+AH < BC +2AH
Vậy AB+AC < BC+ 2AH

A K M I C H B N
a)
Ta có nối K với M
=> Xét t/gMCK và t/gMHC ta có:
CK=CH (gt) hay ^KCM=^MCH (gt)
MC (cạnh chung)
=>t/gMCK = t/gMCH (c.g.c)
=>MK=MH ( tương ứng)
đpcm.
b) Tiếp tục nối K và H
Gọi I là giao điểm của CM và KH
Xét t/gICK và t/gICH ta có:
CK=CH (gt) hay ^HCM=^CMK (gt)
CI (cạnh chung)
=>t/gICK=t/gICH (c.g.c)
=>^CIK=^CIH( tương ứng)
Mà ^CIK+^CIH=180o( góc kề bù)
=>^CIK=^CIH=90o
=>CI_|_HK
=>CM_|_HK
đpcm.
c) Quan sát hình ta thấy ^CMH=65o=^CMN=65o (1)
Vì ^KCM+^MCN=90o
=>^MCN=90o-^KCM
=>^MCN=90o-35o
=>^MCN=65o(2)
Từ (1) và (2) vì ^NMC=^NCM => t/gNMC là t/g cân.
đpcm.

(tự vẽ hình )
câu 4:
a) có AB2 + AC2 = 225
BC2 = 225
Pytago đảo => \(\Delta ABC\)vuông tại A
b) Xét \(\Delta MAB\)và \(\Delta MDC\)
MA = MD (gt)
BM = BC ( do M là trung điểm của BC )
\(\widehat{AMB}=\widehat{CMD}\)( hai góc đối đỉnh )
=> \(\Delta MAB\)= \(\Delta MDC\) (cgc)
c) vì \(\Delta MAB\)= \(\Delta MDC\)
=> \(\hept{\begin{cases}AB=DC\\\widehat{MAB}=\widehat{MDC}\end{cases}}\)
=> AB// DC
lại có AB \(\perp\)AC => DC \(\perp\)AC => \(\Delta KCD\)vuông tại C
Xét \(\Delta\) vuông ABK và \(\Delta\)vuông KCD:
AB =CD (cmt)
AK = KC ( do k là trung điểm của AC )
=> \(\Delta\)vuông AKB = \(\Delta\)vuông CKD (cc)
=> KB = KD
d. do KB = KD => \(\Delta KBD\)cân tại K
=> \(\widehat{KBD}=\widehat{KDB}\)(1)
có \(\Delta ADC\)vuông tại C => \(AD=\sqrt{AC^2+DC^2}=15\)
=> MD = 7.5
mà MB = 7.5
=> MB = MD
=> \(\Delta MBD\)cân tại M
=> \(\widehat{MBD}=\widehat{MDB}\)(2)
Từ (1) và (2) => \(\widehat{KBD}-\widehat{MBD}=\widehat{KDB}-\widehat{MDB}\)hay \(\widehat{KBM}=\widehat{KDM}\)
Xét \(\Delta KBI\)và \(\Delta KDN\)có:
\(\widehat{KBI}=\widehat{KDN}\)(cmt)
\(\widehat{KBD}\)chung
KD =KB (cmt)
=> \(\Delta KBI\)= \(\Delta KDN\)(gcg)
=> KN =KI
=. đpcm
câu 5:
a) Xét \(\Delta ABM\)và \(\Delta MDC\):
MA=MD(gt)
MB=MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{DMC}\)( đối đỉnh )
=> \(\Delta BMA=\Delta CMD\)(cgc)
b) Xét \(\Delta\)vuông ABC
có AM là đường trung tuyến của tam giác
=> \(AM=\frac{1}{2}BC\)mà \(BM=MC=\frac{1}{2}BC\)(do M là trung điểm của BC )
=> AM = BM = MC
có MA =MD => AM = MD =MB =MC
=> BM +MC = AM +MD hay BC =AD
Xét \(\Delta BAC\)và \(\Delta DCA\)
AB =DC
AC chung
BC =DC
=> \(\Delta BAC\)= \(\Delta DCA\)(ccc)
c. Xét \(\Delta ABM\)
BM=AM
\(\widehat{ABM}\)= 600
=> đpcm

Hình tự vẽ.
a) Ta có: AB=AC
\(\Rightarrow\Delta\)ABC cân
Xét \(\Delta\)AHB và \(\Delta\)AHC có:
AHB=AHC (=90o)
AH: chung
ABH=ACH (\(\Delta\)ABC cân)
\(\Rightarrow\)\(\Delta\)AHB=\(\Delta\)AHC (g.c.g)
\(\Rightarrow\)HAB=HAC (2 góc tương ứng)
\(\Rightarrow\)AH là phân giác BAC
b) Xét \(\Delta\)AHK và \(\Delta\)AHQ có:
AKH=AQH (=90o)
AH: chung
HAK=HAQ (cm câu a)
\(\Rightarrow\Delta\)AHK=\(\Delta\)HAQ (ch-gn)
Ta có:
AK+KB=AB
AQ+QC=AC
Mà AB=AC (gt)
AK=AQ (\(\Delta\)AHK=\(\Delta\)AHQ)
\(\Rightarrow\)KB=QC
Xét \(\Delta\)KBH và \(\Delta\)QCH có:
HK=HQ (\(\Delta\)AHK=\(\Delta\)AHQ)
HB=HC (\(\Delta\)AHB=\(\Delta\)AHC)
KB=QC (cmt)
\(\Rightarrow\Delta\)KBH=\(\Delta\)QCH (c.c.c)
\(\Rightarrow\)HK=HQ (2 cạnh tương ứng)
c) Xét \(\Delta\)KBM và \(\Delta\)QCN có:
KMB=QNC (=90o)
KB=QC (cmt)
KBM=QCN (\(\Delta\)ABC cân)
\(\Rightarrow\Delta\)KBM=\(\Delta\)QCN (ch-gn)
\(\Rightarrow\)KM=QN (2 cạnh tương ứng)
Mới làm đc 1 cách :))

Bài 1) .
Ta có : AB =AC ( gt)
=> ∆ABC cân tại A
=> B = C
Xét ∆ ABE và ∆ ACD ta có
AD = DE ( gt)
AB = AC ( gt)
B = C ( cmt)
=> ∆ABE = ∆ACD ( c.g.c)
=> EAB = DAC (dpcm)
b) Vì M là trung điểm BC
=> BM = MC
Mà ∆ABC cân tại A ( cmt)
=> AM là trung tuyến ∆ABC
=> AM là trung tuyến đồng thời là đường cao và phân giác ∆ABC
Mà D,E thuộc BC
AM vuông góc với DE
Mà ∆ADE cân tại A ( AD = AE )
=> AM là đường cao đồng thời là phân giác và trung tuyến ∆ ADE
=> AM là phân giác DAE
c) Vì AM là phân giác DAE
=> DAM = EAM = 60/2 = 30 độ
= > Mà AM vuông góc với DE (cmt)
=> AME = AMD = 90 độ
=> AME + MAE + AEM = 180 độ
=> AEM = 180 - 90 - 30 = 60 độ
Mà ∆ADE cân tại A
=> ADE = AED = 60 độ
Bài 2)
Trong ∆ABC có A = 90 độ
=> BAC = 90 độ :))))))

Cho tam giác abc vuông cân ở a ,m là trung điểm của bc, điểm e nằm giữa m và c.Ke bh,ck vuông với ae (h,k€ae) chứng minh bh=ak.C/m tam giác mbh= tam giác mak.C/m tam giác mhklaf tam giác vuông cân .Vex hình luôn cho mình mình cần gấpkhoang 6 tiênd nữa