Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tg AMB và EMC có :
MA=ME(gt)
MB=MC(gt)
\(\widehat{AMB}=\widehat{CME}\left(đđ\right)\)
=> Tg AMB=EMC(c.g.c) (đccm)
b) Do tg AMB=EMC (cmt)
\(\Rightarrow\widehat{B}=\widehat{ECM}\)
=> AB//EC
\(\Rightarrow\widehat{BAC}=\widehat{ECA}=90^o\)
\(\Rightarrow AC\perp CE\left(đccm\right)\)
c) Do tg ABM=CEM (cmt)
\(\Rightarrow AM=MC=\frac{BC}{2}\)
Hay nói cách khác : BC=2AM (đccm)
#H

Lời giải:
a.
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)

A B E M C K I
a) Xét: "tam giác" ABM và "tam giác" EMC có:
- AM = ME ( gt )
- BM = CM ( gt )
- "góc" AMB = "góc" CME ( đối đỉnh )
=> "Tam giác" ABM = "Tam giác" EMC ( c.g.c )
b) Ta có: "tam giác" AMB = "Tam giác" EMC nên "góc" BAM = "góc" AEC
Mặt khác: hai góc BAM và AEC nằm ở vị trị so le trong
=> AB // CE
c) Xét : "tam giác" AIB và "tam giác" CIK có:
- AI = IC ( gt )
- BI = IK ( gt )
- "góc" AIB = "góc" CIK ( đối đỉnh )
=> "tam giác" AIB = " tam giác" CIK ( c.g.c )
=> "góc" BAI = "góc" KCI ( 2 góc tương ứng )
=> KC // AB
Theo tiên đề ơ- clit về hai đường thẳng song song thì qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó:
Mà: AB // CE (theo b) và KC // AB (cmt)
Nên: E, K, C thẳng hàng
____________________ End _________________________
Mình nghĩ vậy ... không biết có đúng không :) còn mấy chữ nằm trong ngoặc kép ( " " ) bạn thay bằng kí hiệu nha, mình không biết viết kí hiệu ...... hì hì

a)xét tam giác ABM và tam giác DCM có:
BN=CM(GT)
góc BMA=góc CMD(đđ)
AM-DM(GT)
\(\Rightarrow\)tam giác ABM=tam giác DCM(c.g.c)
b)theo câu a: tam giác ABM=tam giác DCM
\(\Rightarrow\)góc BAM= góc MDC(2 góc tương ứng)
mà đây là cặp góc so le trong
\(\Rightarrow\)AB//CD
\(\Rightarrow\)góc BAC= góc ACD=90 độ\(\Rightarrow\)CD \(\perp\)AC
c) xét tam giác AHC và tam giác EHC có:
AH=EH(GT)
góc AHC=góc EHC=90 độ
HC chung
\(\Rightarrow\)tam giác AHC = tam giác EHC(c.g.c)
\(\Rightarrow\)CA=CE(2 cạnh tương ứng)
\(\Rightarrow\)tam giác CAE cân tại C

Ta có hình vẽ:
A B C M E a/ Xét tam giác AMB và tam giác CME có:
BM = MC (GT)
AM = ME (GT)
\(\widehat{AMB}\) =\(\widehat{CME}\) (đối đỉnh)
=> tam giác AMB = tam giác CME (c.g.c)
=> AB = CE (2 cạnh tương ứng) (đpcm)
b/ Ta có:
AM = MC (vì tam giác AMB = tam giác CME)
=> tam giác AMC là tam giác cân vì AM = MC
=> \(\widehat{MAC}\)=\(\widehat{MCA}\) (vì tam giác AMC cân) (1)
Mà \(\widehat{MAB}\)=\(\widehat{MCE}\) (tam giác AMB = tam giác CME) (2)
Từ (1), (2) => \(\widehat{A}\) =\(\widehat{C}\)
Mà \(\widehat{A}\)= 900 => \(\widehat{C}\) = 900
Vậy CE \(\perp\)AC (đpcm)
c/ Xét tam giác ABC và tam giác CEA có:
AB = CE (câu a)
AC: chung
\(\widehat{A}\)=\(\widehat{C}\) = 900 (đã chứng minh)
Vậy tam giác ABC = tam giác CEA (c.g.c)

a, tam giác ABC vuông tại A (gt) => BC^2 = AC^2 + AB^2 (pytago)
BC = 10; AB = 8 (Gt)
=> AC^2 = 10^2 - 8^2
=> AC^2 = 36
=> AC = 6 do AC > 0
b, xét tam giác AMB và tam giác DMC có : AM = MD (gt)
BM = MC do M là trung điểm của BC(gt)
^BMA = ^DMC (đối đỉnh)
=> tam giác AMB = tam giác DMC (c-g-c)
=> ^ABM = ^MCD mà 2 góc này slt
=> AB // CD
AB _|_ AC
=> CD _|_ AC
c, xét tam giác ACE có : AH _|_ AE
AH = HE
=> tam giác ACE cân tại C
d, xét tam giác BMD và tam giác CMA có L BM = MC
AM = MD
^BMD = ^CMA
=> tam giác BMD = tam giác CMA (c-g-c)
=> BD = AC
AC = CE do tam giác ACE cân tại C (câu c)
=> BD = CE
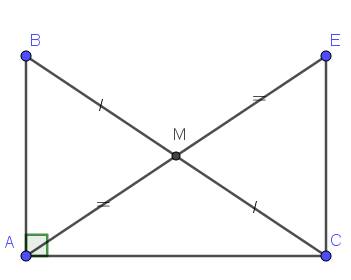
A B C E M
a) Xét t/giác AMB và t/giác EMC
có MA = ME (gt)
BM = MC (gt)
\(\widehat{AMB}=\widehat{EMC}\)(đối đỉnh)
=> t/giác AMB = t/giác EMC (c.g.c)
b) Do t/giác AMB = t/giác EMC (cmt)
=> \(\widehat{BAM}=\widehat{MEC}\)(2 góc t/ứng)
mà 2 góc này ở vị trí so le trong
=> AB // CE
=> \(\widehat{A}+\widehat{C}=180^0\) (trong cùng phía)
mà \(\widehat{A}=90^0\) => \(\widehat{C}=90^0\) => AC \(\perp\)CE
c) Xét t/giác ABC vuông tại A có AM là đường trung tuyến
=> AM = BM = MC = 1/2BC
=> BC = 2AM
HD C2: CM t/giác ABC = t/giác CEA (C.g.c)
=> BC = EA (2 cạnh t/ứng
=> 1/2BC = 1/2EM
=> 1/2BC = MA (vì EM = MA = 1/2EM)
=> AM = 2BC