Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔABC vuông tại A có AM là trung tuyến
nên BC=2*AM
=>BC=5
AB/BC=4/5
=>AB/5=4/5
=>AB=4
AC=căn 5^2-4^2=3
ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2; CH*CB=CA^2
=>BH=4^2/5=3,2cm; CH=3^2/5=1,8cm
ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>AH*5=4*3=12
=>AH=2,4cm

\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=6,25(cm)
AM=BC/2=3,125(cm)
\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)
\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :
\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)
+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\)
\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :
\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)
\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)
+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :
\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)

Xét tam giác ABH vuông tại H, ta có:
\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)
\(\Rightarrow AB=5\left(cm\right)\)
Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:
\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)
AM là đường trung tuyến trong tam giác vuông ABC
=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)


+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
![]()
+) Áp dụng hệ thức về cạnh và đường cao trng tam giác vuông ABC với AH là đường cao ta có:

+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
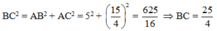
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có:
![]()
+) Diện tích tam giác ABC với AH là đường cao ta có:
![]()
Vậy AB = 5cm, AC = 15 4 cm; AM = 25 8 cm; S ∆ A B C = 75 8 c m 2 .
Đáp án cần chọn là: A

a: AB/AC=3/4
=>BH/CH=9/16
=>BH/9=CH/16=(BH+CH)/(9+16)=125/25=5
=>BH=45cm; CH=80cm
b: AB/AC=3/7
=>HB/HC=(3/7)^2=9/49
=>HB/9=HC/49=k
=>HB=9k; HC=49k
AH^2=HB*HC
=>9k*49k=42^2
=>k=2
=>HB=18cm; HC=98cm
c: Đặt HB/9=HC/16=k
=>HB=9k; HC=16k
AH^2=HB*HC
=>144k^2=48^2
=>k=4
=>HB=36cm; HC=64cm
BC=36+64=100cm
AB=căn 36*100=60cm
AC=căn 64*100=80cm

a: ΔABC vuông tại A có AM là trung tuyến
nên MA=MC=MB
=>góc MAC=góc MCA=góc BAH
b: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
góc EAM+góc AED
=góc AHD+góc MCA
=góc ABC+góc MCA=90 độ
=>AM vuông góc ED
Tự vẽ hình :vv
Áp dụng đ/lý Py-ta-go vào tam giác AHM vuông tại H có:
\(AH^2+HM^2=AM^2\)
\(\Rightarrow12^2+HM^2=13^2\Rightarrow HM=5\left(cm\right)\)
Ta có: tam giác ABC vuông tại A có AM là trung tuyến
\(\Rightarrow AM=\dfrac{1}{2}BC=BM=CM=13cm\)
=> BH=BM-MH=13-5=8(cm)
=> CH=CM+MH=13+5=18(cm)
=> BC=CH+BH=18+8=26 (cm)
Tam giác ABC vuông tại A có AH là đường cao:
\(AB^2=BH.BC=8.26=208\left(cm\right)\) (hệ thức lượng)
\(\Rightarrow AB=4\sqrt{13}\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{26^2-\left(4\sqrt{13}\right)^2}=6\sqrt{13}\left(cm\right)\)