Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)
Xét tam giác vuông CIH và tam giác vuông CBK có:
có góc C chung
=> \(\Delta CIH~\Delta CBK\)( góc -góc)
=> \(\frac{CI}{CB}=\frac{CH}{CK}\Rightarrow CI.CK=CB.CH\) (1)
Mặt khác: Xét tam giác ABC vuoonh tại A và có đường cao AH
=> \(AC^2=CH.CB\)( hệ thức lượng trong tam giác vuông) (2)
Từ (1) và (2) => \(CI.CK=CA^2\)
b) Do D đối xứng với A qua H
=> HA=HD mà AH vuông BC
=> BC là đường trung trực AD
=> AB=DB, AC= DC
Xét tam giác CAB và Tam giác CDB có: BC chung, AB=BD, AC=DC
=> \(\Delta CAB=\Delta CDB\) ( c-c-c)
=> \(\widehat{B_1}=\widehat{B_2}\)(3)
và \(\widehat{CDB}=\widehat{CAB}=90^o\) ( các góc tương ứng bằng nhau)
Xét tứ giác CAKB có: \(\widehat{CAB}=\widehat{CKB}=90^o\)
=> TỨ giác CAKB nội tiếp ( vì có hai góc nội tiếp chắn một cung bằng nhau)
=> \(\widehat{B_1}=\widehat{K_1}\)(4)
Xét tứ giác CKBD có: \(\widehat{CDB}+\widehat{CKB}=90^o+90^o=180^o\)
=> Tứ giác CKBD nội tiếp ( vì có tổng hai góc đối bằng 180^o)
=> \(\widehat{B_2}=\widehat{K_2}\)(5)
Từ (3), (4), (5)
=> \(\widehat{K_2}=\widehat{K_1}\)
=> KC là phân giác góc AKD
Gọi AM cắt DE tại I
Theo tính chất hình chữ nhật ADHE : \(\widehat{E_1}=\widehat{HAC}=\widehat{MBA};\widehat{A_1}=\widehat{D_1}=\widehat{AHE}=\widehat{MCA}\)
\(\Rightarrow\widehat{A_1}=\widehat{ACM}\Rightarrow\Delta ACM\)cân tại M \(\Rightarrow MA=MC\)(*)
Do \(\Delta AID\)vuông tại I suy ra
\(\widehat{DAM}+\widehat{D_1}=90^0\Leftrightarrow\widehat{DAM}+\widehat{DAH}=90^0\left(1\right)\)
\(\widehat{ABM}+\widehat{DAH}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{DAM}=\widehat{ABM}\)
\(\Rightarrow\Delta ABM\)cân tại M \(\Rightarrow MA=MB\)(**)
Từ (*);(**) suy ra MB=MC hay M là trung điểm BC . Do MF//AC suy ra
\(\widehat{MFC}=\widehat{ACF}\)
Mà
\(\widehat{ACF}=\widehat{MCF}\Rightarrow\widehat{MFC}=\widehat{MCF}\Rightarrow\Delta MFC\)cân tại M suy ra MC=MF
Mà MB=MC suy ra 
\(\Delta BFC\) có FM là trung tuyến 
\(FM=\frac{1}{2}BC\Rightarrow\) \(\Delta BFC\)vuông tại F hay 
\(BF\perp CF\left(đpcm\right)\)
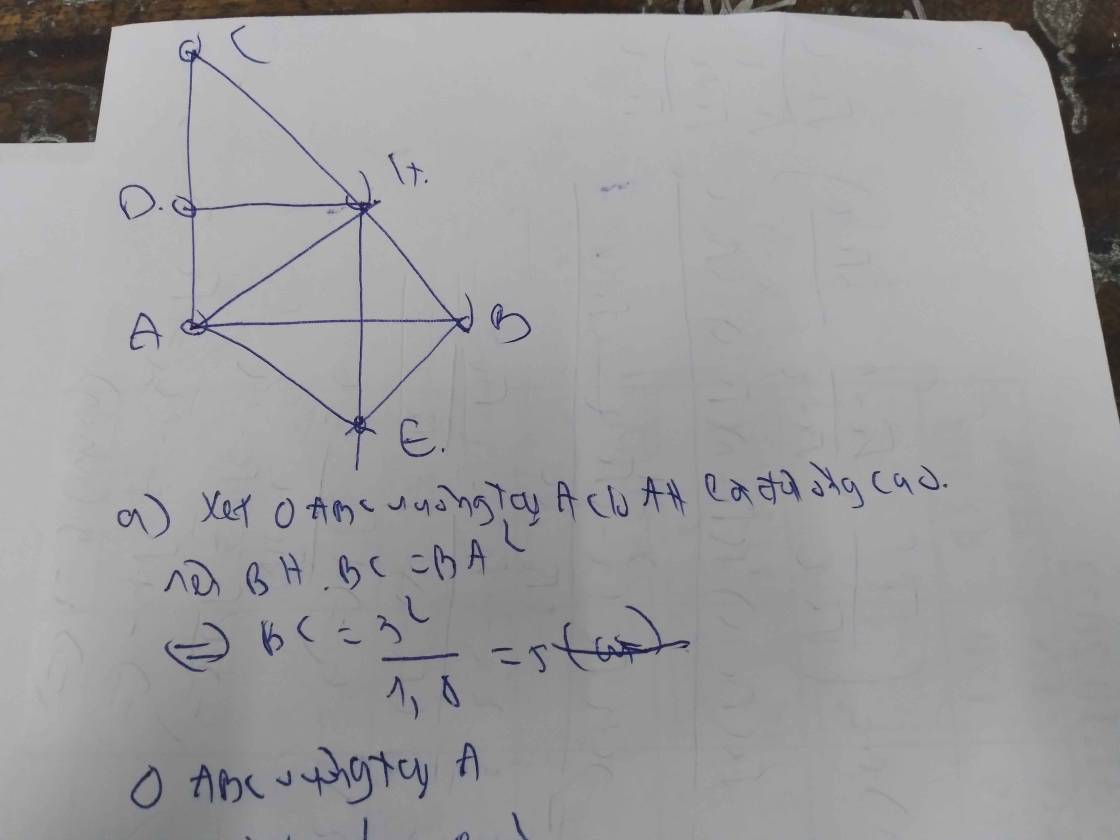
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AB^2=BC^2-AC^2=12^2-8^2=80\)
hay \(AB=4\sqrt{5}cm\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot12=8\cdot4\sqrt{5}=32\sqrt{5}\)
\(\Leftrightarrow AH=\dfrac{32\sqrt{5}}{12}=\dfrac{8\sqrt{5}}{3}cm\)
Vậy: \(AB=4\sqrt{5}cm\); \(AH=\dfrac{8\sqrt{5}}{3}cm\)
c)
Ta có: D và C đối xứng nhau qua A(gt)
nên A là trung điểm của DC
Xét ΔBDC có
BA là đường cao ứng với cạnh DC(BA⊥DC)
BA là đường trung tuyến ứng với cạnh DC(A là trung điểm của DC)
Do đó: ΔBDC cân tại B(Định lí tam giác cân)
⇒\(\widehat{D}=\widehat{C}\)
Xét ΔADE vuông tại E và ΔACH vuông tại H có
AD=AC(A là trung điểm của DC)
\(\widehat{D}=\widehat{C}\)(cmt)
Do đó: ΔADE=ΔACH(cạnh huyền-góc nhọn)
⇒AE=AH(hai cạnh tương ứng)
mà AH là bán kính của đường tròn (A;AH)
nên AE là bán kính của đường tròn (A;AH)
Xét (A;AH) có
AE là bán kính(cmt)
AE⊥BD tại E(gt)
Do đó: BD là tiếp tuyến của đường tròn(A;AH)(Dấu hiệu nhận biết tiếp tuyến đường tròn)
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=25^2-15^2=400\)
=>AC=20(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>AH=12(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{15^2}{25}=9\left(cm\right)\\CH=\dfrac{20^2}{25}=16\left(cm\right)\end{matrix}\right.\)
b: I là trung điểm của AH
=>IA=IH=12/2=6cm
Xét ΔCBK có HI//BK
nên \(\dfrac{HI}{BK}=\dfrac{CH}{CB}\)
=>\(\dfrac{6}{BK}=\dfrac{16}{25}\)
=>\(BK=6\cdot\dfrac{25}{16}=9,375\left(cm\right)\)