
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình vẽ chung cho cả ba bài.
Bài 1:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{15^2}+\frac{1}{20^2}=\frac{1}{144}\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\)
\(\Rightarrow BC=BH+CH=9+16=25\)
Bài 2,3 bạn nhìn hình vẽ và sử dụng hệ thức lượng để tính tiếp như bài 1.
Bài 2: Bài giải
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH\cdot CH\text{ }\Rightarrow\text{ }x\left(25-x\right)=144\text{ }\Rightarrow\text{ }x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\text{ }\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\left(tm\right)\)
Nếu BH = 9 cm thì CH = 16 cm \(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)

VẼ HÌNH HƠI XẤU THÔNG CẢM NHA
áp dụng hệ thức lượng trong tam giác vuông ABC ta có \(AB\cdot AC=AH\cdot BC\) \(\Rightarrow AH\cdot BC=63\) (1)
áp dụng đl pitagovao tam giác vuông ABC ta có \(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{130}\)
thay vao (1) ta co \(AH\cdot BC=63\Rightarrow AH=\frac{63}{\sqrt{130}}\)

Câu 2:
AB/AC=5/6
=>HB/HC=25/36
=>HB/25=HC/36=k
=>HB=25k; HC=36k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>900k^2=900
=>k=1
=>HB=25cm; HC=36cm

Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)


\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)


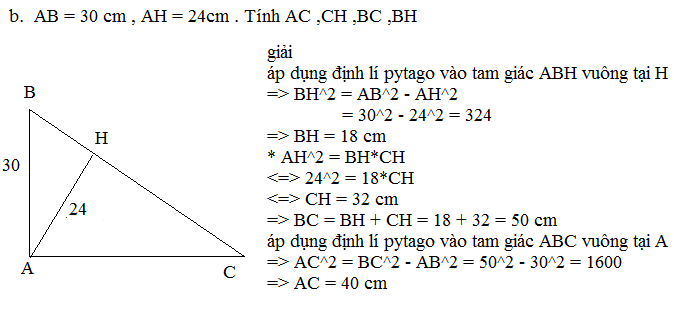
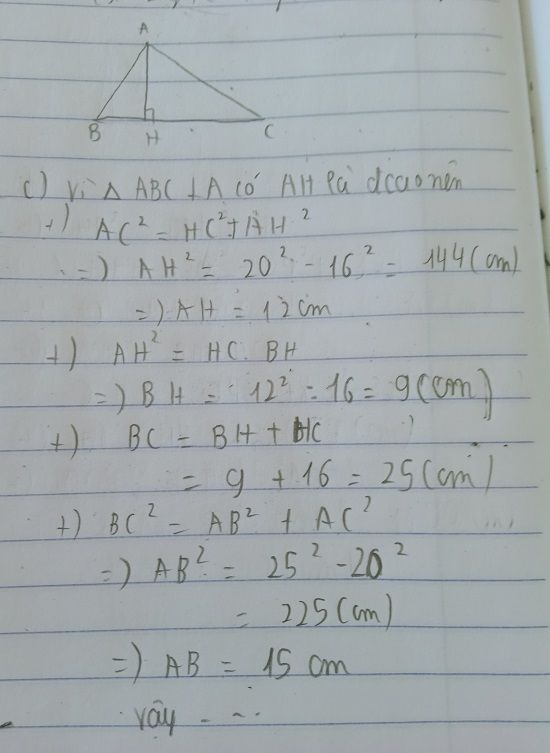
Ta có:
AH.BC=AB.AC
=>AB.AC=192
Mặt khác:AB^2+AC^2=BC^2=20^2
Thế AB=192/AC vào sẽ tìm được: AC=... và AB=......
AB^2=BH.BC=>BH=AB^2/BC=.......(cm)=>CH=.............(cm)'
Tự tính nhé
Ta có:
AH.BC=AB.AC
=>AB.AC=192
Mặt khác:AB^2+AC^2=20^2
Thế AB=192/AC vào sẽ tìm được: AC=... và AB=...(do AC>AB)
AB^2=BH.BC=>BH=AB^2/BC=...(cm)=>CH=...-...=...(cm)