Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
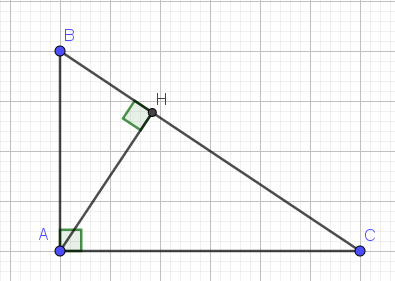
a. Xét tam giác $AHB$ và $CHA$ có:
$\widehat{AHB}=\widehat{CHA}=90^0$
$\widehat{HAB}=\widehat{HCA}$ (cùng phụ với $\widehat{HAC}$)
$\Rightarrow \triangle AHB\sim \triangle CHA$ (g.g)
b.
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
Từ tam giác đồng dạng phần a suy ra $CH=\frac{AH^2}{BH}=\frac{12^2}{9}=16$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)

A B C H 15 12
a, Xét tam giác ABH và tam giác CAH ta có :
^AHB = ^CHA = 900
^BAH = ^HCA ( cùng phụ ^HAC )
Vậy tam giác ABH ~ tam giác CAH ( g.g )
b, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác AHB vuông tại H
\(AB^2=BH^2+AH^2\Rightarrow BH^2=AB^2-AH^2=225-144=81\Rightarrow BH=9\)cm
* Áp dụng hệ thức :
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{144}{9}=16\)cm
=> BC = HC + HB = 16 + 9 = 25 cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AC=\dfrac{AH.BC}{AB}=\dfrac{12.25}{15}=20\)cm
a) Xét ΔBHA vuông tại H và ΔAHC vuông tại H có
\(\widehat{BAH}=\widehat{ACH}\left(=90^0-\widehat{B}\right)\)
Do đó: ΔBHA\(\sim\)ΔAHC(g-g)

a: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=192/20=9,6cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC

a) Xét ΔABC vuông tại B và ΔAHB vuông tại H có
\(\widehat{A}\) chung
Do đó: ΔABC\(\sim\)ΔAHB(g-g)
Suy ra: \(\dfrac{AB}{AH}=\dfrac{AC}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AH\cdot AC\)
b) Ta có: \(AB^2=AH\cdot AC\)
\(\Leftrightarrow AH\cdot12=6^2=36\)
hay AH=3(cm)

Cho Tam giác ABC vuông tại A(AB<AC) có đường cao ah.a chứng minh Tam giác BAH đồng dạng với Tam giác BCA.b vẽ BD là đường phân giác của Tam giác ABC cắt AH tại k. Chứng minh BA.BK=BD.BH.c qua C kẻ đường thẳng vuông góc với BD tại E. Chứng minh AE=EC.
Tam giác ABC vuông
=>
BC2 = AB2 + AC2
AH.BC = AB.AC
=>
BC2 = 225 + AC2
12BC = 15AC
Thay BC = 15AC/12 vào pt trên
=>
81AC2 = 32400
=> AC2 = 400
=> AC = 20cm
=> BC = 25cm
BH = \(\sqrt{AB^2-AH^2}\)= \(\sqrt{15^2-12^2}\)= 9
Ta có:
\(\widehat{AHB}\) = \(\widehat{CHA}\)= 90o (1)
cos (\(\widehat{ABH}\)) = \(\frac{BH}{AB}\)= \(\frac{9}{15}\)= \(\frac{3}{5}\)
cos (\(\widehat{CAH}\)) = \(\frac{AH}{AC}\)= \(\frac{12}{20}\)= \(\frac{3}{5}\)
=> \(\widehat{ABH}\)= \(\widehat{CAH}\)(2)
(1), (2) => Tam giác AHB đồng dạng CHA