Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

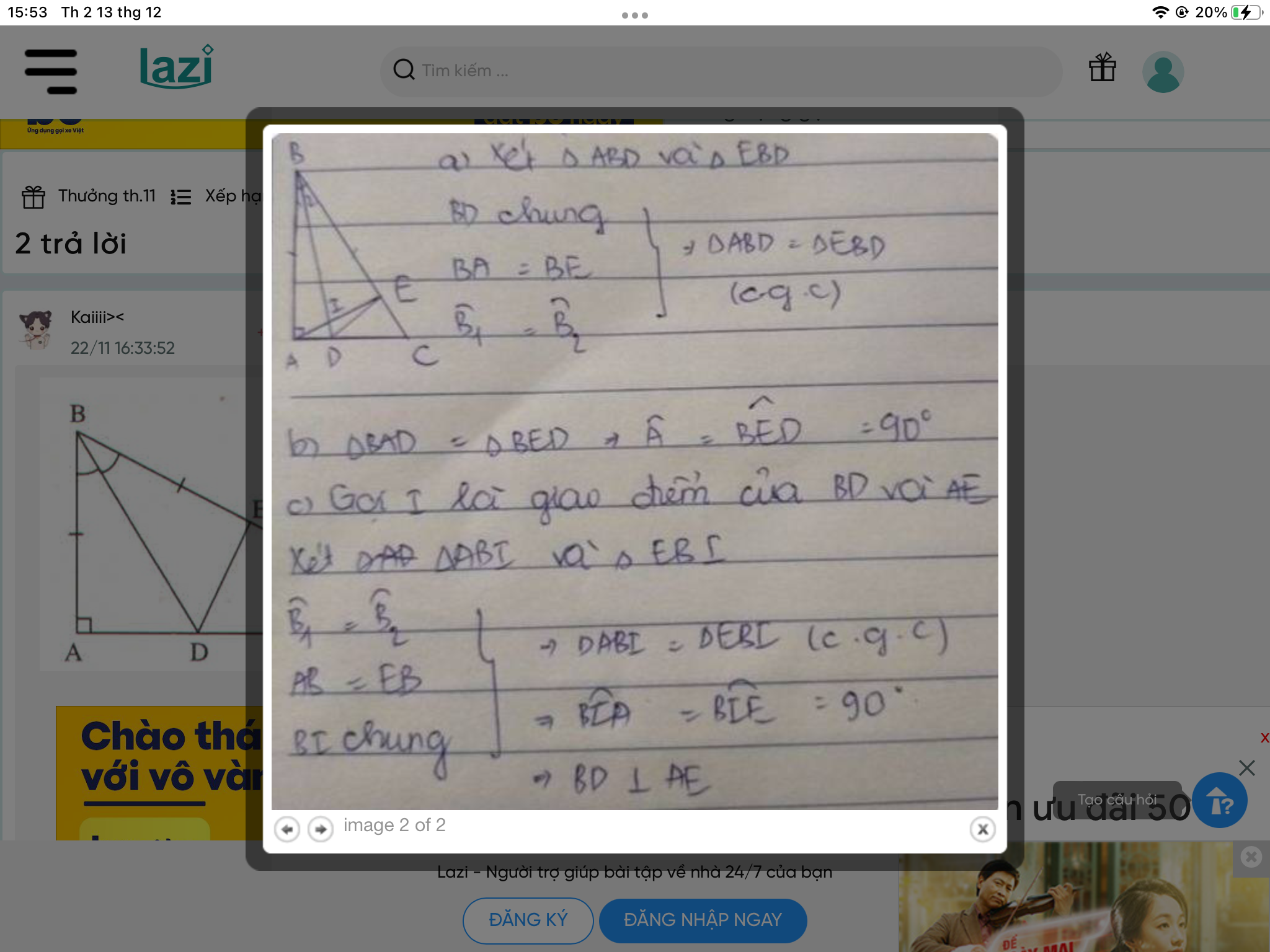
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)

Bài 3:
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra:AC//BD và AC=BD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{CDB}=90^0\)

Answer:
Phần c) thì nhờ các cao nhân khác thoii.
a) Ta xét tam giác ABD và tam giác EBD:
AB = EB (gt)
BD cạnh chung
\(\widehat{B_1}=\widehat{B_2}\)
Vậy tam giác ABD = tam giác EBD (c.g.c)
\(\Rightarrow DE=DA\)
b) Theo phần a), tam giác ABD = tam giác EBD
\(\Rightarrow\widehat{BAD}=\widehat{BED}=90^o\)

a)Xét tam giác ABD và tam giác EBD, có :
AB=EB ( gt)
góc B1= góc B2(BD là p/giác góc ABE) }=>tam giác ABD = tam giác EBD
BD chung
=> AD=DE (2 cạnh tg ứng)
b) Vì tam giác ABD = tam giác EBD (c/m a)
=> góc BAD=góc BED
Mà góc BAD=90 độ
=>góc BED=90 độ
Vây góc BED=90 độ

a) Xét tam giác ABD và tam giác EBD:
+ AB = EB (gt).
+ BD chung.
+ \(\widehat{ABD}=\widehat{EBD}\) (BD là phân giác).
\(\Rightarrow\) Tam giác ABD = Tam giác EBD (c - g - c).
b) Tam giác ABD = Tam giác EBD (cmt).
\(\Rightarrow\) \(\widehat{BAD}=\widehat{BED}\) (2 góc tương ứng).
Mà \(\widehat{BAD}=90^o\) (Tam giác ABC vuông tại A).
\(\Rightarrow\) \(\widehat{BED}=90^o\)
c) Xét tam giác ABE: BA = BE (gt).
\(\Rightarrow\) Tam giác ABE cân tại B.
Mà BD là phân giác (gt).
\(\Rightarrow\) BD là đường cao (Tính chất tam giác cân).
\(\Rightarrow\) \(BD\perp AE.\)

a: \(\widehat{C}=90^0-60^0=30^0\)
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥CB