Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
GIẢI: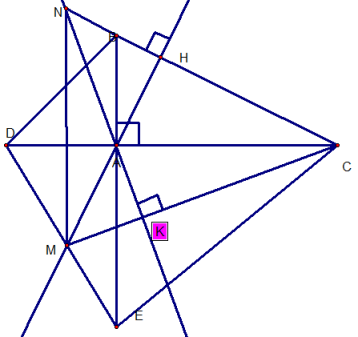
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
câu d:
Tam giác BCF nội tiếp (O;BC/2) có cạnh BC là đường kính
=> Tam giác BCF vuông tại F
=>góc BFC=90 độ
Xét 2 tam giác: tam giác CHF và tam giác CFB có:
góc C chung
góc CHF=góc CFB (=90 độ)
Do đó, tam giác CHF đồng dạng với tam giác CFB (g.g)
=> góc CFH=góc CBF (1)
Tứ giác ABFC nội tiếp (O;BC/2)
=> góc CFH=góc ABC (cùng chắn cung AC) (2)
Từ (1) và (2)=> góc CBF=góc ABC (3)
Mà tia BC nằm giữa tia AB và BF (4)
Từ (3) và (4)=> BC là tia phận giác của góc ABF (đpcm)
Bạn tự vẽ hình :)
a) Ta có : AB = Cos 60 . BC = 1/2 . 12 = 6 cm
AC = Sin 60 . BC = \(\frac{\sqrt{3}}{2}.12=6\sqrt{3}\)
b) BE là tia p/g góc B nên ta có góc ABE = góc EBC = 30 độ
AE = tan 30 . AB = ...
BH = Cos 60. AB = ....
Suy ra AE . AC =BH.BC (bạn tự thay số vào tính)
c) Hãy chứng minh D là trung điểm AH
Sau đó áp dụng tính chất đường trung bình để suy ra DM , DN , MN song song với BC và áp dụng tiên đề Ơ-Clit là ra :)
a) Ta có tứ giác AIMJ là hcn=> AIMJ nội tiếp đường tròn đường kính AM, IJ
Vì N đối xứng với M qua IJ => góc JNI = góc JMI = 90o ha N thuộc đường tròn đường kính AM và IJ => góc ANM = 90o
mà I thuộc trung trực MN => tam giác MIC vuông cân tại I => I thuộc trung trực MC
=> I là tâm đường tròn ngoại tiếp tam giác MNC
=> góc MNC =1/2 góc MIC = 450
=> góc ABC + góc ANC = 45+90+45=1800
Hay tứ giác ABCN nội tiếp đường tròn (T) (ĐPCM)
b)CM: 1/PM<1/PB+1/PC ?
Ta có: tam giác MPC đồng dạng tam giác MBA => PM/MB=PC/BA => PM/PC=MB/BA (1)
TAM GIÁC MBP đồng dạng tam giác MAC => PM/MC=PB/CA=> PM/PB=MC/AC (2)
Cộng vế theo về của (1) và (2) ta có:
PM/PC+PM/PB=MB/BC+MC/AC=MB/BA+MC/BA=AC/BA>1 => ĐPCM
c) Áp dụng hệ thức giữa cạnh và đường cao ta có:
DH2=DK.DC => DA2=DK.DC
=> DA/DC=DK/DA => TAM GIÁC DKA đồng dạng tam giác DAC => góc AKD =DAC =45o
=> góc ABH+ góc AKH = 45+45+90=1800=> TỨ GIÁC ABHK nội tiếp
=> Góc AKB =AHB =90 = GÓC HKC
Mà góc ABK =AHK=KCH => đpcm
a: ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(1\right)\)
Xét ΔADB vuông tại A có AI là đường cao
nên \(BI\cdot BD=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=BI\cdot BD\)
b:
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
Xét ΔABD vuông tại A có \(sinADB=\dfrac{AB}{BD}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH=\dfrac{BA^2}{BC}\)
\(BI\cdot BD=BH\cdot BC\)
=>\(\dfrac{BI}{BC}=\dfrac{BH}{BD}\)
Xét ΔBIH và ΔBCD có
\(\widehat{IBH}\) chung
\(\dfrac{BI}{BC}=\dfrac{BH}{BD}\)
Do đó: ΔBIH đồng dạng với ΔBCD
=>\(\dfrac{BH}{BD}=\dfrac{HI}{CD}\)
\(sinADB\cdot sinACB\)
\(=\dfrac{AB}{BD}\cdot\dfrac{AB}{BC}\)
\(=\dfrac{AB^2}{BD\cdot BC}=\dfrac{BH}{BD}\)
\(=\dfrac{HI}{CD}\)