Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Ta có: \(R=\dfrac{abc}{4S};r=\dfrac{S}{p}\)
Vì tam giác ABC vuông cân tại A nên \(b=c\) và \(a=\sqrt{b^2+c^2}=b\sqrt{2}\)
Xét tỉ số:
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}.\left(b.c\right)^2}=\dfrac{a\left(a+2b\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)

\(\cos ABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(\Leftrightarrow89a^2-AC^2=2\cdot5a\cdot8a\cdot\dfrac{1}{2}=40a^2\)
=>AC=7a
\(AM=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{25a^2+49a^2}{2}-\dfrac{64a^2}{4}=37a^2-16a^2=21a^2\)
hay \(AM=a\sqrt{21}\left(cm\right)\)

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{1}{32}\)
\(\Rightarrow A\approx92^0\)
\(p=\dfrac{AB+AC+BC}{2}=\dfrac{31}{2}\)
\(S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\simeq40\)
\(r=\dfrac{S}{p}=\dfrac{80}{31}\)
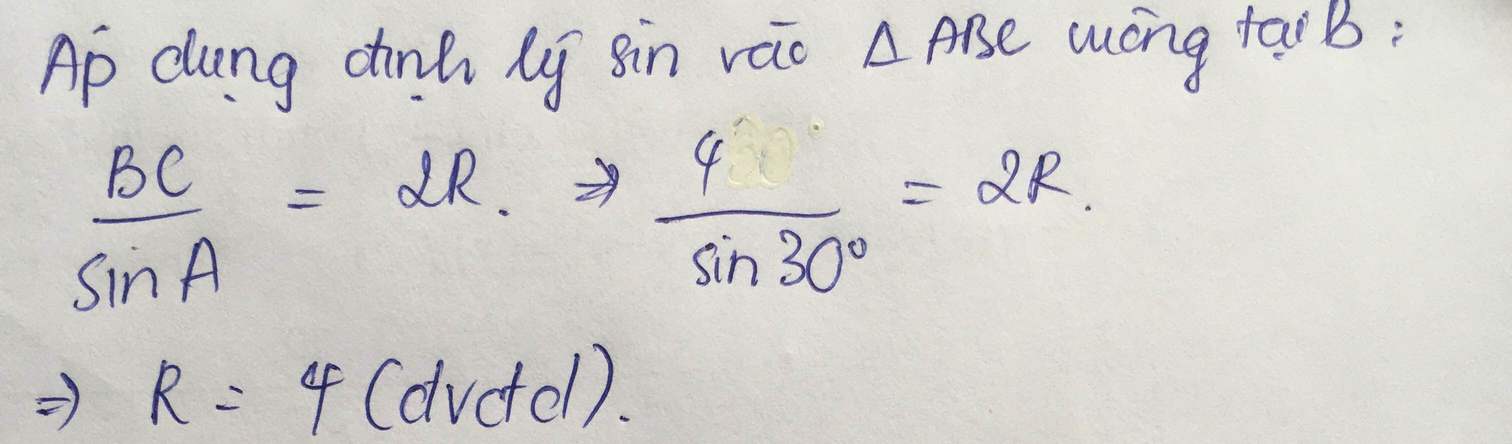
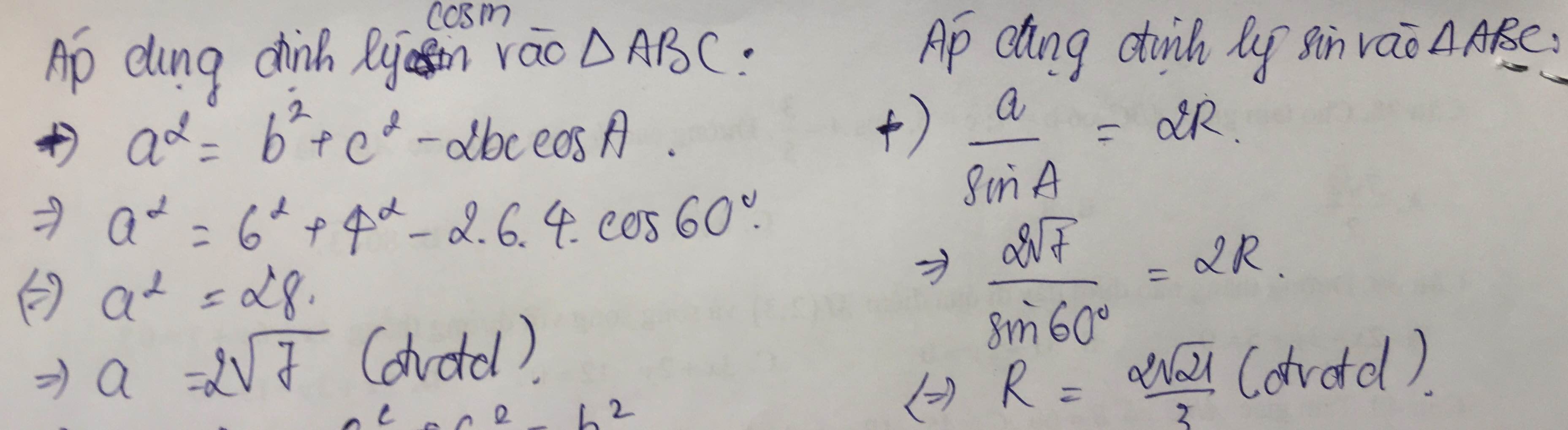
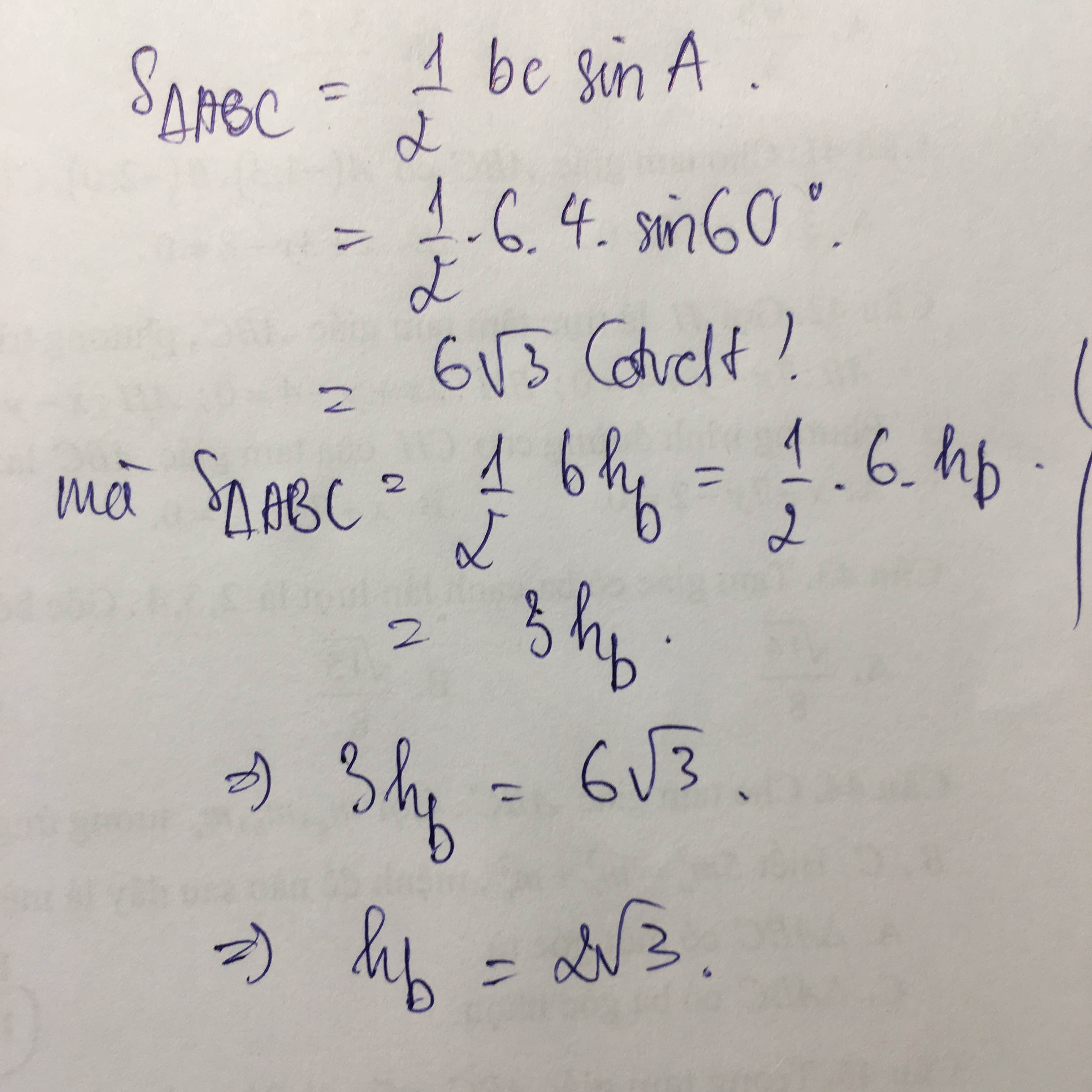
Xét ΔABC vuông tại A có
\(cosB=\dfrac{AB}{BC}\)
=>\(\dfrac{4}{BC}=sin60=\dfrac{1}{2}\)
=>BC=8(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+4^2=8^2=64\)
=>\(AC^2=48\)
=>\(AC=4\sqrt{3}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot4\cdot4\sqrt{3}=8\sqrt{3}\)
Nửa chu vi tam giác ABC là:
\(4+4\sqrt{3}+8=12+4\sqrt{3}\)
Bán kính đường tròn nội tiếp ΔABC là:
\(\dfrac{8\sqrt{3}}{12+4\sqrt{3}}=\dfrac{2\sqrt{3}}{\sqrt{3}+3}=\sqrt{3}-1\)