
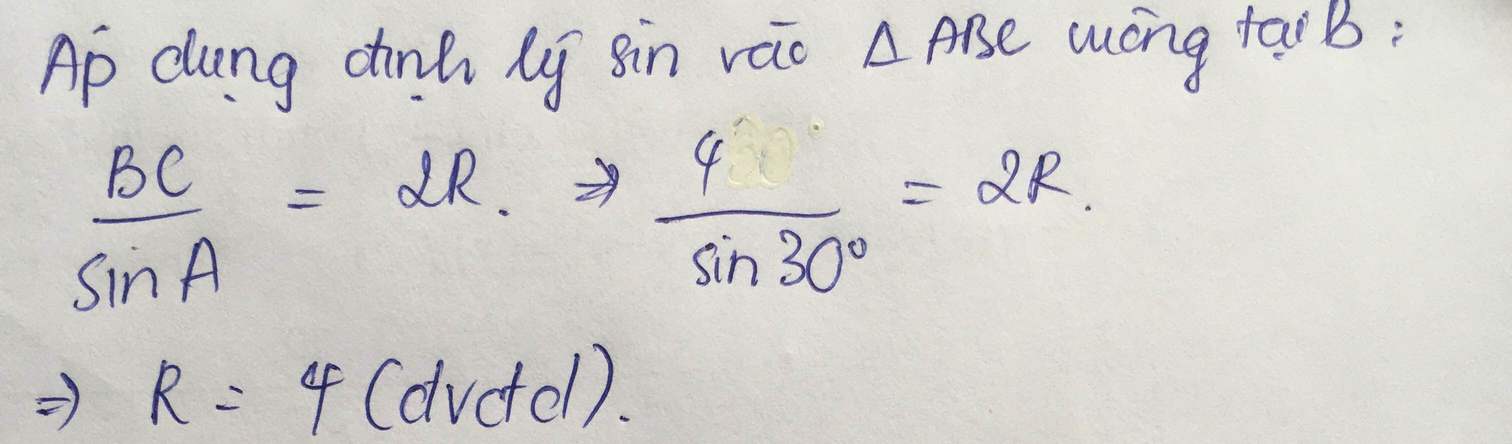
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

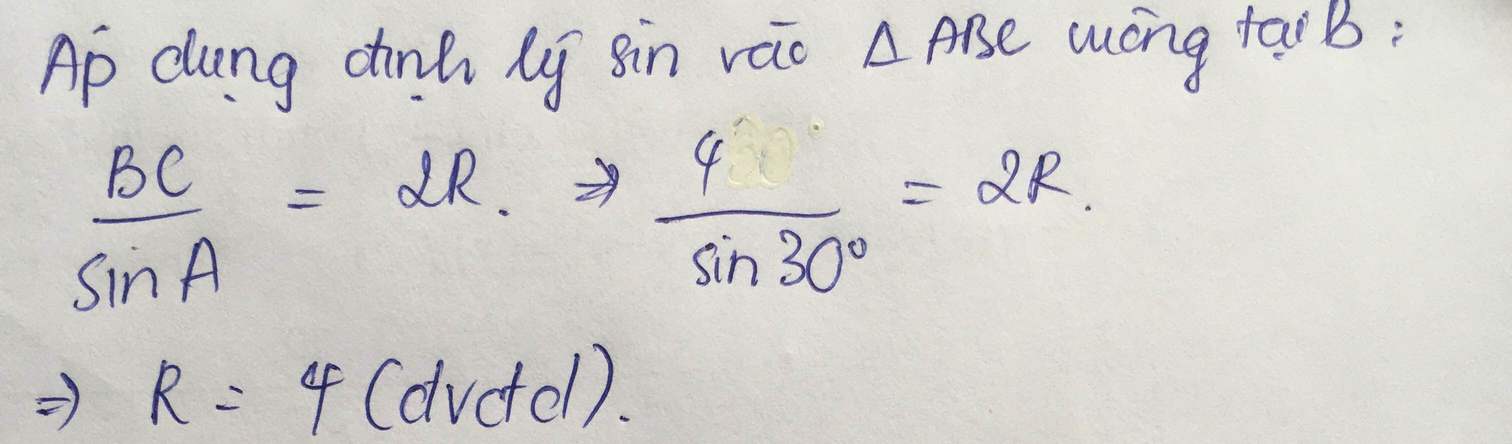

\(\cos ABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(\Leftrightarrow89a^2-AC^2=2\cdot5a\cdot8a\cdot\dfrac{1}{2}=40a^2\)
=>AC=7a
\(AM=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{25a^2+49a^2}{2}-\dfrac{64a^2}{4}=37a^2-16a^2=21a^2\)
hay \(AM=a\sqrt{21}\left(cm\right)\)

a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
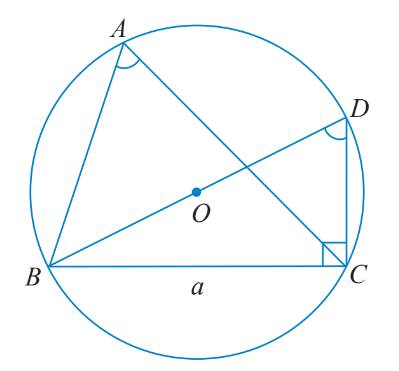
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
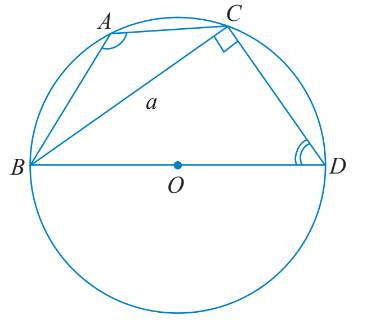
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)

Xét tam giác ABC có đường cao BH:
cos ABC = \(\dfrac{7^2+15^2-13^2}{2\cdot7\cdot15}\) = \(\dfrac{1}{2}\) \(\Rightarrow\) \(\widehat{ABC}=60^o\)
\(p=\dfrac{13+7+15}{2}=17,5\) (cm)
Hê-rông: \(S=\sqrt{17,5\cdot\left(17,5-13\right)\cdot\left(17,5-7\right)\cdot\left(17,5-15\right)}\approx45,5\) (cm2)
\(S=\dfrac{abc}{4R}\) \(\Rightarrow\) \(R=\dfrac{abc}{4S}\approx\dfrac{13\cdot7\cdot15}{4\cdot45,5}=7,5\) (cm)
\(S=\dfrac{1}{2}BH\cdot AC\) \(\Rightarrow\) \(BH=\dfrac{2S}{AC}\approx\dfrac{2\cdot45,5}{13}=7\) (cm)
Chúc bn học tốt!

Ta có công thức tính diện tích tam giác khi biết các cạnh của tam giác và bán kính đường tròn ngoại tiếp là:
\(S=\frac{abc}{4R}\); với R là bán kính đường tròn ngoại tiếp và; a, b, c lần lượt là các cạnh của tam giác.
Bài giải:
A B C H
Ta có tam giác AB=AC =10 cm
Kẻ đường cao BH
=> BH= CH= 12:2 =6cm
Áp dụng định lí Pitago
=> AH^2 =AC^2-HC^2=10^2-6^2=64
=> AH = 8 cm
=> Diện tích tam giác ABC: S= AH.BC:2=48 (cm^2)
Mặt khác \(S=\frac{AB.AC.BC}{4R}\Rightarrow R=\frac{AB.AC.BC}{4S}=\frac{10.10.12}{4.48}=6,25\left(cm\right)\)
Vậy bán kính đường tròn ngoại tiếp bằng 6,25 cm.

Áp dụng định lý Sin trong tam giác ABC ta có:
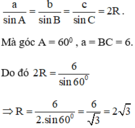
Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.