Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)

a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
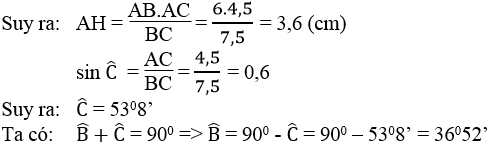 b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.

#)Giải :
a)\(\Delta ABC\)vuông tại A (gt) \(\Rightarrow\widehat{BAD}+\widehat{DAC}=90^o\left(1\right)\)
\(\Delta HAD\)vuông tại H (gt)\(\Rightarrow\widehat{HDA}+\widehat{HAD}=90^o\left(2\right)\)
Vì AD là tia phân giác của \(\widehat{HAC}\Rightarrow\)\(\widehat{HAD}=\widehat{DAC}\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{BAD}=\widehat{DAC}\)
\(\Rightarrow\Delta ABD\)cân tại A
b) Từ cmt \(\Rightarrow AB=BD\)(tính chất của tam giác cân)
Đặt \(AB=BD=x\)
Áp dụng hệ thức lượng trong tam giác vuông ABC
\(\Rightarrow AB^2=HB.HC\)
Hay \(x^2=\left(x-6\right)25\)
\(\Rightarrow x^2-25+150=0\)
\(\Rightarrow\left(x-10\right)\left(x-15\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-10=0\\x-15=0\end{cases}\Rightarrow\orbr{\begin{cases}x=10\\x=15\end{cases}}}\)
Vậy AB = 10 hoặc AB = 15
