Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giác AHC và tam giác AHC có: AH chung
AB = AC do tam giác ABC cân tại A (gt)
góc AHB = góc AHC = 90
=> tam giác AHC = tam giác AHC (ch-cgv)
b, tam giác AHC = tam giác AHC (câu a)
=> CH = BH (đn)
xét tma giác BHN và tam giác CHM có: góc MHC = góc NHB (đối đỉnh)
HN = HM (gt)
=> tam giác BHN = tam giác CHM (c-g-c)
=> góc BNH = góc HMC (đn) mà 2 góc này slt
=> BN // AC (đl)

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: góc ABH+góc EBC=góc ABC
góc ACK+góc ECB=góc ACB
mà góc ABH=góc ACK;góc ABC=góc ACB
nên góc EBC=góc ECB
=>ΔEBC cân tại E
c: AB=AC
EB=EC
=>AE là trung trực của BC
=>AE vuông góc với BC

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>HB=HC
=>BC=2HB
ΔAHB vuông tại H nên AB^2=AH^2+HB^2
=>HB^2=5^2-4^2=9
=>HB=3(cm)
=>BC=2*3=6cm
c: Xét ΔBAK có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAK cân tại B

B1:tự vẽ hình:>
b,Xét t/g vg ABH và t/g vg ACK có
AB=AC(vì t/g ABC cân)
Góc A chung
=>t/g ABH=t/g ACK(ch-gn)
c,Ta có:AK+KB=AB
AH+HC=AC
Mà AB=AC,AK=AH(t/gABH=t/gACK)
=>KB=HC(1)
Mặt khác:K1+K2=H1+H2=180o
Mà K1=H1
=>K2=H2(2)
Vì t/g ABH=t/g ACK(cmt)
=>Góc ABH=góc ACK(2 góc t.ư) (3)
Từ(1),(2) và (3)=>t/g OBK=t/g OCH(g.c.g)
c,chưa nghĩ ra
B2,Tự vẽ hình
a,t/g ABC cân tại A
=>Góc ABC=góc ACB(1)
EI // AF => góc EIB = góc ACB(2)
Từ (1) và (2)=>góc ABC=góc EIB
=>t/g BEI cân tại E
b,t/g BEI cân tại E
=>BE=EI mà BE=CF
=>CF=EI
Xét t/g IEO và t/g CFO có
CF=EI
Góc IDE=góc COF (đối đỉnh)
góc CFI=góc OEI
=>t/gIEO=t/gCFO(g.c.g)
=>OE=OF(2 cạnh t.ư)
c,Ta có :ABKC là hình thoi(ABK=ACK=90o)
Mà t/g ABC là t/g cân tại A
=>t/g BKC cân tại K=>BK=KC
Xét t/g CFK và t/g BEK có:
BK=KC
EBK=OCF
CF=BE
=>t/g CFK=t/g BEK(g.c.g)
=>t/g EKF cân tại K
Có OE=OF(cm ở câu b)
=>Ok là trung tuyến EKF
=>OK là trung trực
=>OK vuông EF

a)Xét ∆ABC và ∆AMC ta có:
AB = AM (GT)
^A1=^A2= 90 độ (GT)
AC là cạnh chung
Do đó: ∆ABC = ∆AMC (c.g.c)


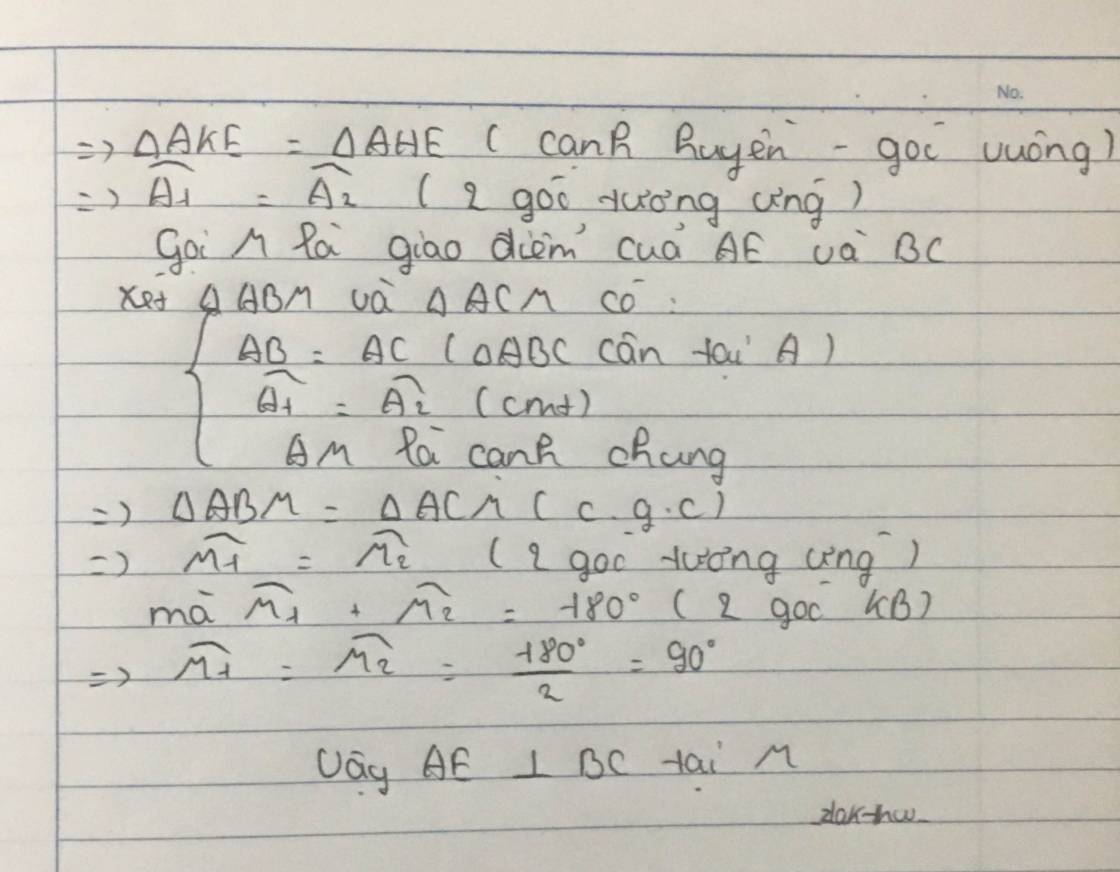
tam giác ABN cân tại B nên đường cao cũng chính là đường trung tuyến nên AH =HN
Ta có : hai tam giác ABH và NBH có BH là cạnh chung ,NB=BA ,AH=HN nên hai tam giác bằng nhau theo trường hợp cạnh cạnh cạnh