Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì BM là đường phân giác của góc B nên ta có:
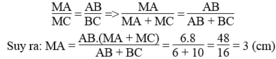
Vì BN là đường phân giác của góc ngoài đỉnh B nên ta có: BM ⊥ BN
Suy ra tam giác BMN vuông tại B
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: A B 2 = AM.AN
Suy ra: AN = ![]() = 12 (cm)
= 12 (cm)


Áp dụng định lý Pitago cho ABH vuông tại A có:
![]()
![]()
Vì BM là tia phân giác trong của góc B ⇒ M A M C = A B B C (Tính chất đường phân giác)
⇒ M A M C + M A = A B B C + A B ⇒ M A A C = A B B C + A B ⇒ M A 8 = 6 10 + 6 ⇒ MA = 3cm
Vì BM; BN là tia phân giác trong và ngoài của góc B ⇒ N B M ^ = 90 0
Áp dụng hệ thức lượng trong ABM vuông tại B có đường cao BA ta có:
![]()
Đáp án cần chọn là: D

Vì BM là đường phân giác của góc B nên ta có :
\(\frac{MA}{MC}=\frac{AB}{BC}\Rightarrow\frac{MA}{MA+MC}=\frac{AB}{AB+AC}\)
\(\Rightarrow MA=\frac{AB.\left(MA+MC\right)}{AB+BC}=\frac{6.8}{6+10}=\frac{48}{16}=3\left(cm\right)\)
Vì BN là đường phân giác của góc ngoài đỉnh B nên ta có: \(BM\perp BN\)
Suy ra tam giác BMN vuông tại B
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: AB2 = AM . AN
Suy ra: \(AN=\frac{AB^2}{AM}=\frac{6^2}{3}=\frac{36}{3}=12\left(cm\right)\)
Tính được mỗi AM , AN nên thông cảm 😅
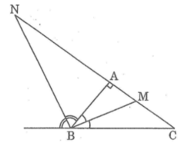

Tam giác ABC vuông ở A có AB=6dm ,AC=8dm nên BC= 10 dm (Pytago)
Vì BM là p/g trong của tg ABC nên \(\frac{AM}{AB}\)= \(\frac{MC}{BC}\)(t/c p/g trong của tam giác)
\(\frac{AM}{AB}\)= \(\frac{MC}{BC}\)= \(\frac{AM+MC}{AB+BC}\)=\(\frac{AC}{AB+BC}\)=\(\frac{8}{6+10}\)=\(\frac{1}{2}\)( tính chất dãy tỉ số bằng nhau)
\(\frac{AM}{6}\)= \(\frac{1}{2}\)\(\Rightarrow\)AM= 3 dm.
Vì BM, BN lần lượt là p/g trong và ngài của góc B của tg ABC nên BN\(⊥\)BM
Xét tg BMN vuông tại B có BA là đườngcao( BA\(⊥\)AChay BA\(⊥\)MN) có
BA\(^2\)=NA*AM \(\Leftrightarrow\)6\(^2\)= AN*3 \(\Rightarrow\)AN= 12(dm).
Vậy AM=3(dm), AN=12(dm)
thks nha