Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(cot\alpha=\dfrac{5}{12}\)
\(\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{12}\Leftrightarrow\dfrac{AC}{30}=\dfrac{5}{12}\)
\(\Rightarrow AC=\dfrac{5\cdot30}{12}=12,5\left(cm\right)\)
Ta có \(\Delta ABC\) vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC=\sqrt{AC^2+AB^2}=\sqrt{30^2+12,5^2}=32,4\left(cm\right)\)

\(a,\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{5}{12}\Leftrightarrow AC=\dfrac{5}{12}\cdot6=2,5\left(cm\right)\\ b,BC=\sqrt{AC^2+AB^2}=\sqrt{2,5^2+6^2}=6,5\left(cm\right)\left(pytago\right)\)
a) Xét tam giác ABC vuông tại A:
\(AC=tan\alpha.AB=\dfrac{5}{12}.6=2,5\left(cm\right)\)
b) Áp dụng đ/lý Pytago trong tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{2,5^2+6^2}=6,5\left(cm\right)\)

ta có \(\sin B=\frac{AC}{BC}=\frac{12}{15}=\frac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=90^o-\widehat{B}\approx37^o\)
... Py-ta-go \(\Rightarrow AB^2=BC^2-AC^2=15^2-12^2=9^2\)
\(\Rightarrow AB=9cm\)
b, gọi BD là x .Áp dụng tc đường phân giác ta có:
\(\frac{AB}{AC}=\frac{BD}{CD}=\frac{x}{BC-x}\)(x<15)
\(\Rightarrow\frac{9}{12}=\frac{x}{15-x}\Rightarrow x=\frac{45}{7}cm\)
Hệ thức lượng \(\Rightarrow AB.AC=BC.AH\Rightarrow AH=\frac{AC.AB}{BC}\)\(\Rightarrow AH=\frac{9.12}{15}=7,2\left(cm\right)\)
.... Py-ta-go: \(\Rightarrow BH^2=AB^2-AH^2=9^2-7,2^2=29,16\)
\(\Rightarrow BH=5,4cm\)
do AB<AC nên H nằm giữa B và D
\(\Rightarrow HD=BD-BH=\frac{45}{7}-5,4=\frac{36}{35}\left(cm\right)\)
... py ta go..\(AD^2=HD^2+AH^2=\left(\frac{36}{35}\right)^2+7,2^2\)
\(\Rightarrow AD^2=\frac{2592}{49}\Rightarrow AD=\frac{36\sqrt{2}}{7}cm\)
Bạn tự kết luận nha! hồi nãy mk đã gửi một bài chi tiết hết sức rồi mà olm lại báo có lỗi xảy ra nên ko gửi lên được!
Mấy cái chỗ .... thì bạn tự điền thêm vào nha!
k cho mk là được rồi! mk ko cần thẻ! cám ơn!
ta có \(\sin B=\frac{AC}{BC}=\frac{12}{15}=\frac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=90^o-\widehat{B}\approx37^o\)
... Py-ta-go \(\Rightarrow AB^2=BC^2-AC^2=15^2-12^2=9^2\)
\(\Rightarrow AB=9cm\)
b, gọi BD là x .Áp dụng tc đường phân giác ta có:
\(\frac{AB}{AC}=\frac{BD}{CD}=\frac{x}{BC-x}\)(x<15)
\(\Rightarrow\frac{9}{12}=\frac{x}{15-x}\Rightarrow x=\frac{45}{7}cm\)
Hệ thức lượng \(\Rightarrow AB.AC=BC.AH\Rightarrow AH=\frac{AC.AB}{BC}\)\(\Rightarrow AH=\frac{9.12}{15}=7,2\left(cm\right)\)
.... Py-ta-go: \(\Rightarrow BH^2=AB^2-AH^2=9^2-7,2^2=29,16\)
\(\Rightarrow BH=5,4cm\)
do AB<AC nên H nằm giữa B và D
\(\Rightarrow HD=BD-BH=\frac{45}{7}-5,4=\frac{36}{35}\left(cm\right)\)
... py ta go..\(AD^2=HD^2+AH^2=\left(\frac{36}{35}\right)^2+7,2^2\)
\(\Rightarrow AD^2=\frac{2592}{49}\Rightarrow AD=\frac{36\sqrt{2}}{7}cm\)
Bạn tự kết luận nha! hồi nãy mk đã gửi một bài chi tiết hết sức rồi mà olm lại báo có lỗi xảy ra nên ko gửi lên được!
Lần 2 nó lại bảo phải kiểm duyệt trước khi hiển thị! Ức chế hết sức!!! chương trình này có lẽ lỗi nặng?
Mấy cái chỗ .... thì bạn tự điền thêm vào nha!
k cho mk là được rồi! mk ko cần thẻ! cám ơn!

Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:
![]()
Trong tam giác vuông ABC vuông tại A có AH là đường cao
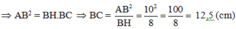
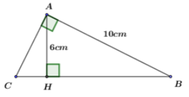
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
![]()
Vậy AC = 7,5 (cm); BC = 12,5 (cm)
Đáp án cần chọn là: B

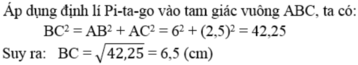
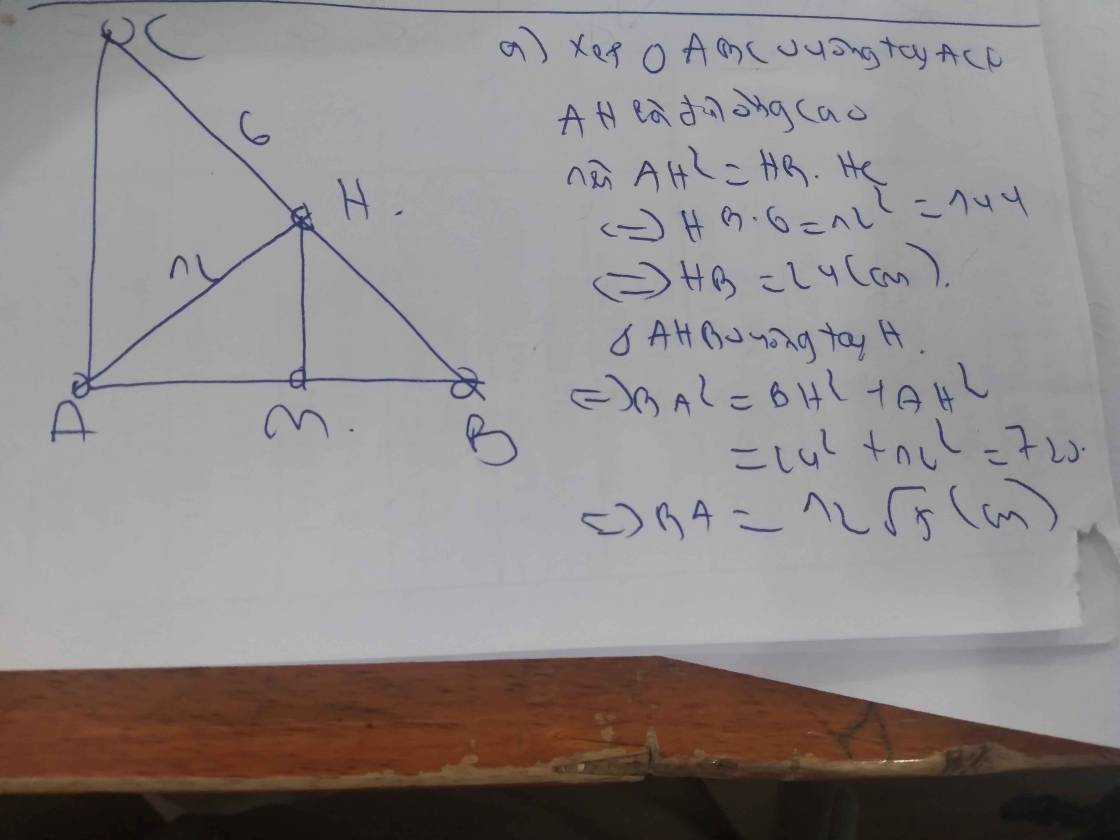
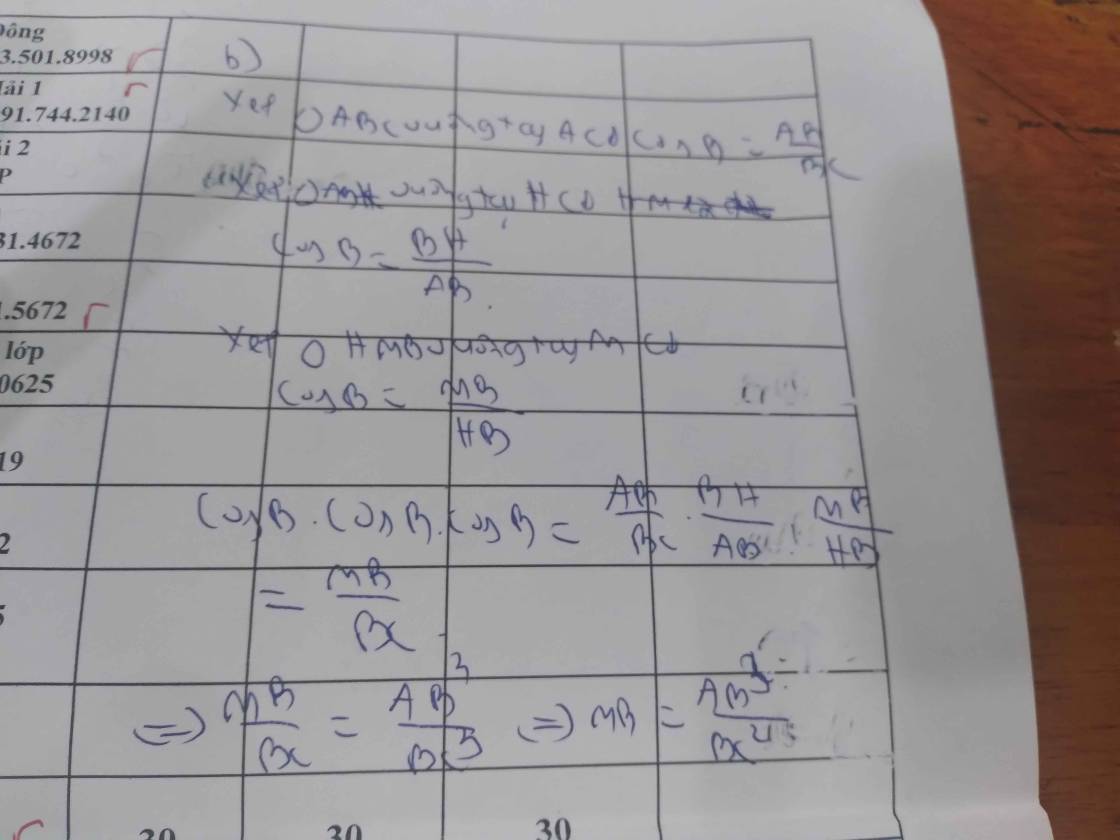
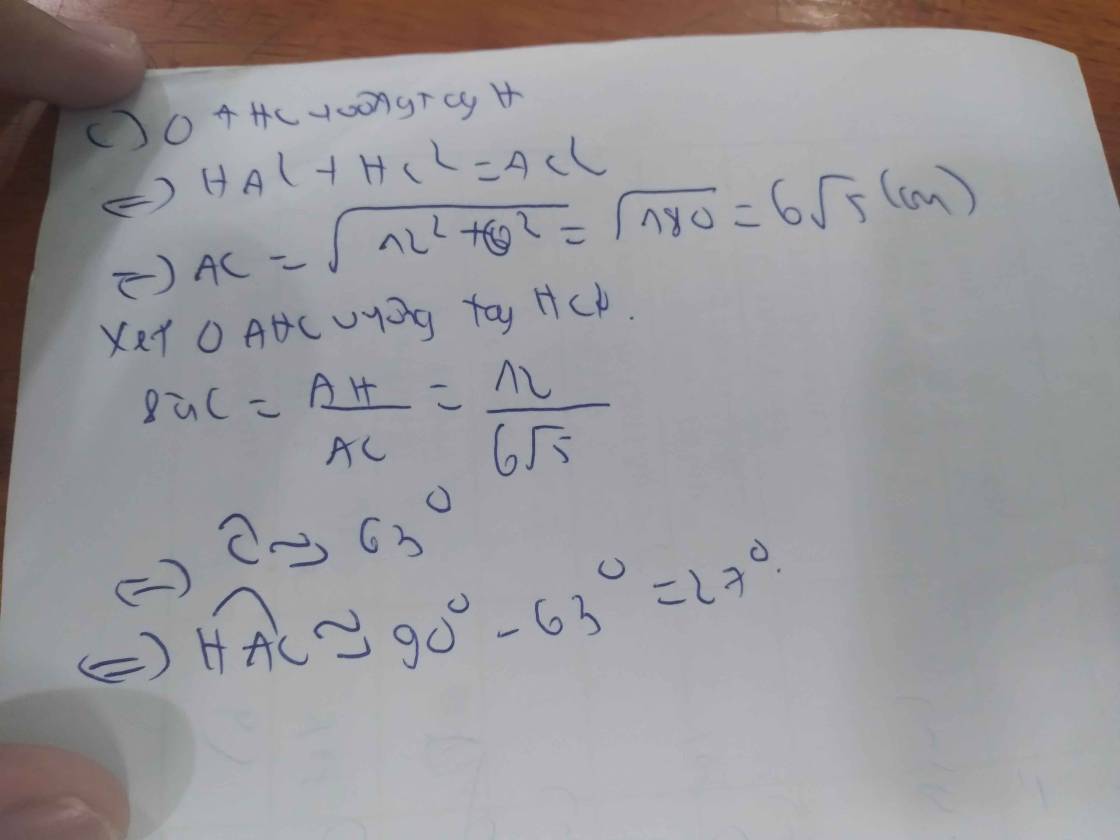
Tam giác ABC vuông tại A ta có:
\(tanB=\dfrac{AC}{AB}=>\dfrac{5}{12}=\dfrac{AC}{6}=>AC=\dfrac{5\cdot6}{12}=\dfrac{5}{2}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(AB^2+AC^2=BC^2\\ =>BC=\sqrt{AB^2+AC^2}\\ =>BC=\sqrt{6^2+\left(\dfrac{5}{2}\right)^2}=\dfrac{13}{2}\left(cm\right)\)
Để giải bài toán, ta cần sử dụng một số công thức và định lý trong hình học, đặc biệt là định lý Pythagore và định nghĩa của các hàm số lượng giác.
Cho tam giác ABC vuông tại A, với AB = 6 cm và tanα = 5/12. Góc B = α.
a) Tính độ dài cạnh AC
Vì tam giác vuông tại A, góc α là góc B, ta có:
tan(α)=đoˆˊi diệnkeˆˋ\tan(\alpha) = \frac{\text{đối diện}}{\text{kề}}tan(α)=keˆˋđoˆˊi diện
Trong tam giác ABC vuông tại A:
tan(α)=BCAC\tan(\alpha) = \frac{BC}{AC}tan(α)=ACBC
Theo đề bài, tan(α)=512\tan(\alpha) = \frac{5}{12}tan(α)=125.
Do đó, ta có:
BCAC=512\frac{BC}{AC} = \frac{5}{12}ACBC=125
Từ đó suy ra:
BC=512ACBC = \frac{5}{12} ACBC=125AC
b) Tính độ dài cạnh BC
Ta sử dụng định lý Pythagore cho tam giác ABC vuông tại A:
BC2=AB2+AC2BC^2 = AB^2 + AC^2BC2=AB2+AC2
Đầu tiên, ta cần tính AC.
Biết rằng tan(α)=512\tan(\alpha) = \frac{5}{12}tan(α)=125, do đó ta có:
sin(α)=BCBC2+AC2\sin(\alpha) = \frac{BC}{BC^2 + AC^2}sin(α)=BC2+AC2BC sin(α)=BCBC2+AC2\sin(\alpha) = \frac{BC}{BC^2 + AC^2}sin(α)=BC2+AC2BC
Vì tan(α) = 5/12 nên ta đặt BC = 5k và AC = 12k. Vì thế:
BC=5kBC = 5kBC=5k
AC=12kAC = 12kAC=12k
Sử dụng định lý Pythagore:
BC2=AB2+AC2BC^2 = AB^2 + AC^2BC2=AB2+AC2
(5k)2=AB2+(12k)2(5k)^2 = AB^2 + (12k)^2(5k)2=AB2+(12k)2
25k2=62+144k225k^2 = 6^2 + 144k^225k2=62+144k2
25k2=36+144k225k^2 = 36 + 144k^225k2=36+144k2
Từ đó, ta có:
AC=12k5AC = \frac{12k}{5}AC=512k
AC2=AB2+BC2AC^2 = AB^2 + BC^2AC2=AB2+BC2
(12k)2=62+(5k)2(12k)^2 = 6^2 + (5k)^2(12k)2=62+(5k)2
144k2=36+25k2144k^2 = 36 + 25k^2144k2=36+25k2
144k2−25k2=36144k^2 - 25k^2 = 36144k2−25k2=36
119k2=36119k^2 = 36119k2=36
k2=36119k^2 = \frac{36}{119}k2=11936
k=36119k = \sqrt{\frac{36}{119}}k=11936
k=6119k = \frac{6}{\sqrt{119}}k=1196
BC=5k=5×6119=30119BC = 5k = 5 \times \frac{6}{\sqrt{119}} = \frac{30}{\sqrt{119}}BC=5k=5×1196=11930
AC=12k=12×6119=72119AC = 12k = 12 \times \frac{6}{\sqrt{119}} = \frac{72}{\sqrt{119}}AC=12k=12×1196=11972
Chúng ta có thể tính toán lại bằng cách:
Suy ra: BC=512ACBC = \frac{5}{12} ACBC=125AC AC=12×65=14.4AC = \frac{12 \times 6}{5} = 14.4AC=512×6=14.4 BC=5×1.2=6BC = 5 \times 1.2 = 6BC=5×1.2=6
Suy ra:...