Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tự xét tam giác zuông ABD = tam giác zuông MBD( cạnh huyền - góc nhọn )
=>AB=AM
=> Tam giác ABM cân
b)Tự xét tam giácAEC= ENC
=>CN=CA
khi đó AB+AC=BM+CN
=> BM+MC+MN=BC+MN
=>MN=AB+BC-BC
c) tam giác AMB cân
=> góc AMB =\(\frac{180^0-\widehat{ABC}}{2}=90^0-\frac{\widehat{ABC}}{2}\)
từ ANC cân ở N ( tự cm)
=> góc ANB =180-góc ACB /2=90 độ -ACB/2
trong tám giác AMN có
\(\widehat{MAN}=180^0-\widehat{AMB}-\widehat{ANC=180^0-\left(90^0-\frac{\widehat{ABC}}{2}\right)-\left(90^0-\frac{\widehat{ACB}}{2}\right)}\)
=>\(\widehat{\widehat{MAN}=\frac{\widehat{ABC}}{2}+\frac{ACB}{2}=\frac{90}{2}=45^0}\)
zì tam giác ABC zuông tại A nên góc ABC +ACB=90 độ
d) zì tam giac AMB cân ở B nên đường phân giác BD đồng thời là đường cao
=>BD\(\perp AM\)hay \(GI\perp AK\)
Mặt khác tam giác ANC cân ở C ( cái này cậu tự cm ở trên mình bảo ấy )
do đó đường phân giác CE đồng thời là đường cao
=>\(CE\perp AN=>KI\perp AG\)
trong tam giác AKG có 2 đường cao xuất phát từ G , K cắt nhau tại I
=> I là trực tâm của tam giác AKG
=>\(AI\perp GK\)ở H nên góc AHG=90 độ

a) xét tam giác ABD và tam giác BMD có:
góc B1 = góc B2 (gt)
BD chung
góc A = góc M = 900
=> tam giác ABD = tam giác BMD (g.c.c)
=> AB = BM (cạnh tương ứng)
=> tam giác ABM cân tại B
b) bó tay

4,
a/ tgiác ACD và tgiác AME là hai tgiác vuông tại A.
AD = AE (gt)
góc(ADC) = góc (AEM) (góc có cạnh tương ứng vuông góc)
=> tgiácACD = tgiácAME (g.c.g)
b/ ta có: AG//EH (cùng vuông góc với CD)
=> AG // IH
mà gt => AI // GH
vậy AGHI là hình bình hành
=>AG = IH.
mặt khác theo cm trên ta có: tgiác ACD = tgiác AME
=> AM = AC = AB
=> A là trung điểm BM, mà AI // BC
=> AI là đường trung bình của tgiác MBH
=> I là trung điểm của MH.
vậy: IM = IH = AG
có: AM = AB
góc BAG = góc AMI (so le trong)
=> tgiác AGB = tgiác MIA ( c.g.c)
c/ có AG//MH, A là trung điểm BM
=> AG là đường trung bình của tgiácBMH
=> G là trung điểm BH
hay BG = GH.

A B C D E i H
A) Ta có tam giác ABC cân
=> AB = AC
Mà AD + DB = AB
AE + EC = AC
=> DB = EC ( AD = AE gt)
b) đề phải là BE và CD cắt nhau tại I
Ta có AD = AE
=> Tam giác ADE cân tại A
=> Góc ADE = Góc AED
=> Góc EDB = Góc DEC ( Cùng cộng nhau bằng 180 độ )
Xét Tam giác DEB và tám giác EDC có
BD = EC (cmt)
Góc EDB = Góc DEC (cmt)
DE là cạnh chung
=> Tam giác DEB và tam giác EDC (c-g-c)
=> Góc DBE = Góc ECD
=> Góc IBC = Góc ICB ( cùng cộng góc DBE và Góc ECD bằng hai góc ABC và Góc ACB)
=> Tam giác IBC cân
c) Ta có tam giác ADE cân \(\Leftrightarrow\widehat{ADE}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Và tam giác ABC cân \(\Leftrightarrow\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2)\(\Leftrightarrow\widehat{ADE}=\widehat{ABC}\)
Hai góc này ở vị trí đồng vị bằng nhau
=> DE // BC (đpcm)
d) Ta có điểm I cách đều cạnh AB và AC
=> AI là tia phân giác của tam giác ABC
trong tam giác cân tia phân giác cũng là đường cao
=> AI vuông góc với BC
E) chứng minh HI là tia phân giác của tam giác BHC
thì ba điểm thẳng hàng

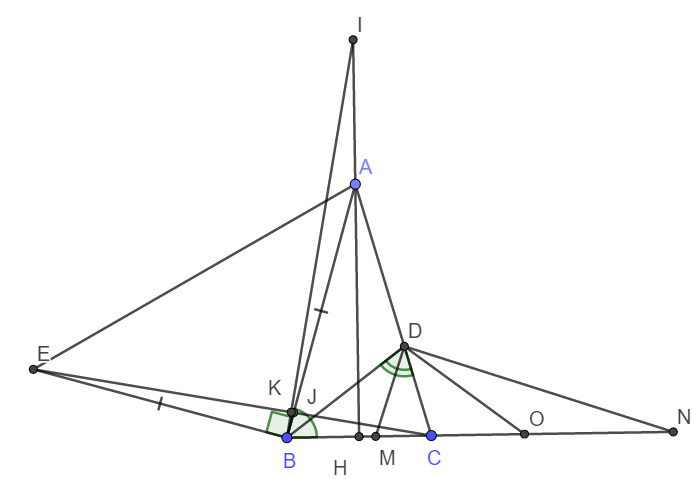
a)
+) Do tam giác ABC cân tại A nên trung tuyến AH đồng thời là đường caio.
Vậy nên \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
+) Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
b) Gọi O là trung điểm MN. Ta thấy DN và DM là phân giác của hai góc kề bù nên chúng vuông góc với nhau.
Vậy tam giác DMN vuông tại D. Khi đó ta có DO là trung tuyến ứng với cạnh huyền nên DO = MN/2
Vậy DO = OM = OM hay các tam giác DOM và DON cân tại O.
Ta có: \(\widehat{DOM}=180^o-2\widehat{DMO}=180^o-2\left(\widehat{MDB}+\widehat{MBD}\right)\)
\(=180^o-2.\widehat{MDB}-2.\widehat{MBD}=180^o-\widehat{BDC}-\widehat{ABC}\)
\(=180^o-\widehat{BDC}-\widehat{ACB}=\widehat{DBO}\)
Vậy tam giác DBO cân tại D hay DB = DO.
Vậy nên BD = MN/2.
xét tam giác BAI va CBE
be=ab
bc=ia
iab=ebc
=>tam giác BAI=tam giác CBE


hoi ma k co ai tra loi.kakak.nhuc qa lang huyen trang hhee
kệ