Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải : (Mình nêu sơ ý thôi, còn trình bày thì mình không rõ nhé )
SMNPB = 44 (cm2)
hay : a2 = 44
=> a = \(\sqrt{44}\)
a = \(2\sqrt{11}\)
=> MB = MN = NP = BP = \(2\sqrt{11}\)
Có MB = AB/2 (vì M là trung điểm của AB)
=> 2 . \(2\sqrt{11}\) = AB
AB =\(4\sqrt{11}\)
Tính BC bạn cũng làm tương tự như cách trên.
Vì ABC là tam giác vuông
=> AC2 = AB2 + BC2
AC2 = ( \(4\sqrt{11}\)) 2 + (\(4\sqrt{11}\))2
AC2 = 176 + 176
AC2 = 352
AC = \(4\sqrt{22}\)

Bài 1:
A C B
Độ dài cạnh AB: ( 49 + 7 ) : 2 = 28 (cm)
Độ dài cạnh AC: 28 - 7 = 21 (cm)
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AC^2+AB^2\)
Hay \(BC^2=21^2+28^2\)
\(\Rightarrow BC^2=441+784\)
\(\Rightarrow BC^2=1225\)
\(\Rightarrow BC=35\left(cm\right)\)
Bài 2:
A B C D
Áp dụng định lý Py-ta-go vào tam giác ABD vuông tại D có:
\(AB^2=AD^2+BD^2\)
\(\Rightarrow AD^2=AB^2-BD^2\)
Hay \(AD^2=17^2-15^2\)
\(\Rightarrow AD^2=289-225\)
\(\Rightarrow AD^2=64\)
\(\Rightarrow AD=8\left(cm\right)\)
Trong tam giác ABC có:
\(AD+DC=AC\)
\(\Rightarrow DC=AC-AD=17-8=9\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác BCD vuông tại D có:
\(BC^2=BD^2+DC^2\)
Hay \(BC^2=15^2+9^2\)
\(\Rightarrow BC^2=225+81\)
\(\Rightarrow BC^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17,5\left(cm\right)\)

A B C M G
a. áp dụng dl Pytago ta có
BC^2= AB^2+AC^2
BC^2= 8^2+15^2=64+225=289(cm)
=> BC= căn 289=17cm
b. vì trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền nên
AM= 1/2BC= BC/2=8.5cm
AG= 2/3 AM = 2/3 . 8.5 xấp xỉ 5.7

B A C M D E M' a)MD vuông góc với AB --> ^MDA=90 độ
ME vuông góc với AC --> ^MEA=90 độ
Mà ^DAE=90 độ => ADME là hình chữ nhật
Tam giác BDM vuông có ^DMB = 45 độ
=> DM=DB
=>Pdme= 2(DM+DA)=2(DB+DA)=2AB=2AC=8(cm)
b) Gọi M' là chân đường cao hạ từ A xuống BC
Ta có: DE=AM ( ADME là hình chữ nhật)
Mà AM≥AM' (Theo tính chất đường xiên)
=> DEmin khi M là chân đường cao hạ từ A xuống BC

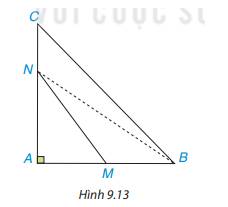
Ta có: Góc NMB là góc ngoài tại đỉnh M của tam giác AMN nên góc NMB là góc tù.
Góc BNC là góc ngoài tại đỉnh N của tam giác ABN nên góc BNC là góc tù.
Xét tam giác MNB có góc NMB là góc tù nên là góc lớn nhất trong tam giác. Cạnh NB đối diện với góc NMB nên là cạnh lớn nhất trong tam giác. Ta được NM < NB.(1)
Xét tam giác CNB có góc BNC là góc tù nên là góc lớn nhất trong tam giác. Cạnh CB đối diện với góc BNC nên là cạnh lớn nhất trong tam giác. Ta được NB < CB.(2)
Từ (1) và (2) ta được NM < CB.
Vậy MN < BC.
\(S_{MNPB}=NP^2=441\Rightarrow NP=21\left(cm\right)\)
MNPB là hình vuông (gt) nên NP = MB = 1/2 AB
\(\Rightarrow\frac{1}{2}AB=21\Rightarrow AB=42\left(cm\right)\)
Áp dụng định lí pitago, ta có:
\(BA^2+BC^2=AC^2\)
\(\Rightarrow2AB^2=AC^2\)
\(\Rightarrow AC^2=2.42^2\Rightarrow AC=42\sqrt{2}\left(cm\right)\)