Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

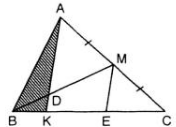
Kẻ đường thẳng qua C vuông góc AC cắt AD tại E
ta có ABCE=BDCD=2ABCE=BDCD=2 (1)
mà AB =AC =2 .AM (2)
từ (1, 2) =>AMCE=1AMCE=1 =>AM =CE
=>△BAM=△ACE△BAM=△ACE (c, g, c)
=>ABMˆ=CAEˆABM^=CAE^
mà ABMˆ+AMBˆ=90∘ABM^+AMB^=90∘
=>CAEˆ+AMBˆ=90∘CAE^+AMB^=90∘
=>BM vuông góc AD(đpcm)
Kẻ DE // BM \(\rightarrow\frac{IM}{DE}=\frac{3}{5},BM=3DE\rightarrow MB=5MI\)
\(AB=a\rightarrow AM=\frac{a}{2},BM^2=\frac{5a^2}{4}\rightarrow MI.MB=\frac{Mb^2}{5}=\frac{a^2}{4}\)
\(AM^2=\frac{a^2}{4}\rightarrow MA^2=MI.MB=\frac{MB^2}{5}=\frac{a^2}{4}\)

a/ Xét tg ADM và tg EDB
Bx//AC \(\Rightarrow\widehat{DAC}=\widehat{DEB}\) (góc so le trong)
\(\widehat{ADM}=\widehat{BDE}\) (góc đối đỉnh)
=> Xét tg ADM đồng dạng tg EDB (g.g.g) \(\Rightarrow\frac{BD}{DM}=\frac{BE}{AM}=\frac{BE}{\frac{AC}{2}}=\frac{1}{2}\Rightarrow\frac{BE}{AC}=\frac{1}{4}\)
b/ Xét tg BKE và tg AKC có
\(\widehat{AKC}=\widehat{BKE}\) (góc đối dỉnh)
Bx//AC \(\Rightarrow\widehat{KAC}=\widehat{KEB}\) (góc so le trong)
=> tg BKE đồng dạng tg AKC (g.g.g) \(\Rightarrow\frac{BE}{AC}=\frac{BK}{KC}=\frac{1}{4}\Rightarrow\frac{BK}{AC}=\frac{1}{5}\left(dpcm\right)\)

Câu hỏi của pham trung thanh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.