Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(AH=\sqrt{1.8\cdot3.2}=2.4\left(cm\right)\)
AB=3(cm)
AC=4(cm)

Ta có: AH^2=9*16=> AH=12
xét tam giac ABH vg có AB^2=AH^+BH^2=>AB=15

Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông:
$144=AH^2=BH.HC(1)$
$BH+CH=BC=25(2)$
Từ $(1); (2)$ áp dụng định lý Viet đảo thì $BH, CH$ là nghiệm của pt: $x^2-25x+144=0$
$\Rightarrow BH, CH= (16,9)$
Mà $AB< AC$ nên $BH< CH$
$\Rightarrow BH=9; CH=16$ (cm)
$AB=\sqrt{BH^2+AH^2}=\sqrt{9^2+12^2}=15$ (cm)
$AC=\sqrt{CH^2+AH^2}=\sqrt{16^2+12^2}=20$ (cm)
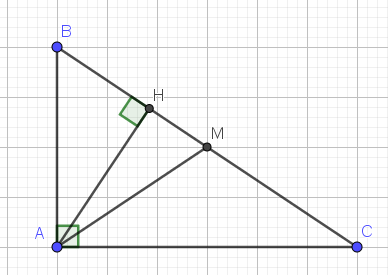
b.
$AM=\frac{BC}{2}=\frac{25}{2}$ (cm)
$\sin \widehat{AMH}=\frac{AH}{AM}=\frac{24}{25}$
$\Rightarrow \widehat{AMH}\approx 74^0$
c.
$HM=\sqrt{AM^2-AH^2}=\sqrt{(\frac{25}{2})^2-12^2}=3,5$ (cm)
$S_{AHM}=\frac{AH.HM}{2}=\frac{12.3,5}{2}=21$ (cm2)

a: Đặt BH=x; CH=y(x<y)
Theo đề, ta có: xy=12^2=144 và x+y=48
=>x,y là các nghiệm của phương trình:
x^2-48x+144=0
=>x=24-12 căn 3 hoặc x=24+12căn 3
=>BH=24-12căn 3 và CH=24+12căn 3
\(AB=\sqrt{\left(24-12\sqrt{3}\right)\cdot48}\simeq12,42\left(cm\right)\)
\(AC=\sqrt{\left(24+12\sqrt{3}\right)\cdot48}\simeq46,36\left(cm\right)\)
b: AM=BC/2=24cm
sin AMH=AH/AM=12/24=1/2
=>góc AMH=30 độ

a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>AC=căn 16=4
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=12/5=2,4
b: Ta có: ΔBAE cân tại B
mà BC là đường cao
nên BC là phân giác của góc ABE
Xét ΔBAC và ΔBEC có
BA=BE
\(\widehat{ABC}=\widehat{EBC}\)
BC chung
Do đó: ΔBAC=ΔBEC
=>\(\widehat{BAC}=\widehat{BEC}\)
=>\(\widehat{BEC}=90^0\)
=>CE\(\perp\)EB tại E
Xét (B) có
BE là bán kính
CE vuông góc BE tại E
Do đó: CE là tiếp tuyến của (B;BA)
ΔCBA=ΔCBE
=>CA=CE
mà CA=4
nên CE=4

Tam giac ABC đồng dạng tam giác HAC (cùng vuông và có chung góc C)
AB/AC = AH/HC = 20/21
HC = 21AH/20 = 441
==> AC = căn(AH^2 + HC^2) =căn(420^2 + 441^2) = 609
AB/AC = 20/21
AB = 20/21*609 = 580
BC = căn(AB^2 + AC^2) = căn(580^2 + 609^2) = 841
Chu vi tam giác ABC = tổng 3 cạnh
C = AB + AC + BC = 580 + 609 + 841 = 2030

\(BC=BH+CH=18+32=50\left(cm\right)\)
Ta có tam giác ABC vuông tại A có AH là đường cao nên:
\(\left\{{}\begin{matrix}AB=\sqrt{BH\cdot BC}=\sqrt{18\cdot50}=30\left(cm\right)\\AC=\sqrt{CH\cdot BC}=\sqrt{32\cdot50}=40\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{30\cdot40}{50}=24\left(cm\right)\)
Mà I là trung điểm của AH nên:
\(IA=IH=\dfrac{1}{2}\cdot AH=\dfrac{1}{2}\cdot24=12\left(cm\right)\)
Xét tam giác IBH vuông tại H có:
\(tanBIH=\dfrac{BH}{IH}\)
\(\Rightarrow\widehat{BIH}=tan^{-1}\dfrac{BH}{IH}=tan^{-1}\dfrac{18}{12}\approx56^o\)
Mà: \(\widehat{BIH}+\widehat{AIB}=180^o\)
\(\Rightarrow\widehat{AIB}=180^o-56^o\approx124^o\)

AH=2,4 nhé
(Tự vẽ hình nhé )
Áp dụng dụng định lí Pytagov vào tam giác ABC vuông tại A có:
\(AB^2+AC^2=BC^2\)
⇔ BC = 2√5
\(\cos ACB\) = \(\dfrac{4}{2\sqrt{5}}\) = 26 độ