Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng phương trình theo đoạn chắn của
mặt phẳng và áp dụng BĐT Bunhiacopski.
Chọn A.

a) \(\Delta ABC\) cân tại A nên AH là đường cao đồng thời cũng là trung tuyến.
\(\Rightarrow BH=\frac{1}{2}BC=\frac{1}{2}.6=3\left(cm\right)\)
Xét \(\Delta ABH\) vuông tại H có:
\(AH^2+BH^2=AB^2\) (Định lý Py-ta-go)
\(\Rightarrow AH^2+3^2=5^2\)
\(\Rightarrow AH^2=5^2-3^2=26-9=16\)
Mà \(AH>0\Rightarrow AH=4\left(cm\right)\)
Vậy \(BH=3\) \(cm;\) \(AH=4\) \(cm.\)
b) G là trọng tâm \(\Delta ABC\), nên G nằm trên đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow G\in AH\)
\(\Rightarrow A,G,H\) thẳng hàng.
Vậy \(A,G,H\) thẳng hàng.
c) \(\Delta ABC\) cân tại A nên AH là đường cao đồng thời là phân giác góc BAC
\(\Rightarrow AG\) là phân giác góc BAC
\(\Rightarrow\) Góc BAG = góc CAG
Xét \(\Delta BAG\) và \(\Delta CAG\), ta có:
\(AB=AC\) ( \(\Delta ABC\) cân tại A)
Góc BAG = góc CAG (Chứng minh trên)
Cạnh AG chung
\(\Rightarrow\Delta BAG=\Delta CAG\left(c.g.c\right)\)
\(\Rightarrow\) Góc ABG = góc ACG (hai góc tương ứng)
Vậy góc ABG = góc ACG.

a,Ta có:AD vuông góc với BC(gt)
BE vuông góc với AD(gt)
Mà AD cắt BE tại H (gt)
Từ đó suy ra H là trực tâm
Mà H thuộc CH,suy ra CH vuông góc AB

Đáp án B
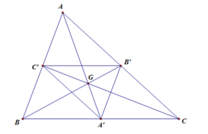
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C
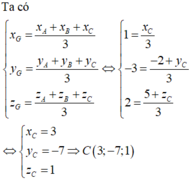
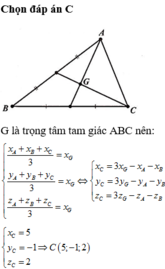
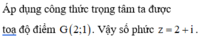
\(\overrightarrow{OG}=\dfrac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}\)
=>\(\overrightarrow{OG}+\overrightarrow{GA}+\overrightarrow{OG}+\overrightarrow{GB}+\overrightarrow{OG}+\overrightarrow{GC}=3\cdot\overrightarrow{OG}\)
=>\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
=>G là trọng tâm của ΔABC