
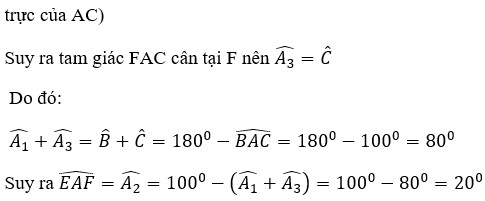
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


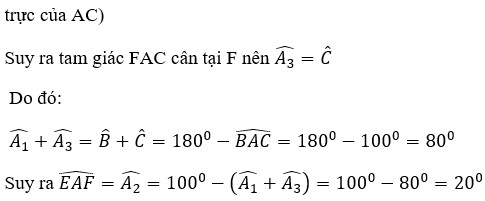

a)\(\widehat{C}=\widehat{BAH}=90^O-\widehat{CAH}\)
\(\widehat{B}=\widehat{CAH}=90^O-\widehat{BAH}\)
b)Ta có:
\(\widehat{ADC}=\widehat{B}+\widehat{BAD}=\widehat{B}+\frac{\widehat{BAH}}{2}=\widehat{B}+\widehat{\frac{C}{2}}\)
Lại có:
\(\widehat{DAC}=180^O-\widehat{C}-\widehat{ADC}=180^O-\widehat{C}-\left(\widehat{B}+\widehat{\frac{C}{2}}\right)=\left(90^O-\widehat{B}\right)-\frac{\widehat{C}}{2}+\left(90^O-\widehat{C}\right)\)
\(=\widehat{C}-\widehat{\frac{C}{2}}+\widehat{B}=\widehat{B}+\frac{\widehat{C}}{2}\)
Suy ra:\(\widehat{ADC}=\widehat{DAC}\)
\(\Rightarrow\Delta ADC\)cân tại C
c)\(DK\perp BC;AH\perp BC\Rightarrow DK//AH\)
\(\Rightarrow\widehat{KDA}=\widehat{DAH}\)(hai góc so le trong)
Mà \(\widehat{BAD}=\widehat{DAH}\)
\(\Rightarrow\widehat{BAD}=\widehat{KDA}\)
\(\Rightarrow\)\(\Delta KAD\)cân tại K
d)Xét \(\Delta CDK-\Delta CAK\)
\(\hept{\begin{cases}CD=CA\\KD=KA\\CA.chung\end{cases}}\)
\(\Rightarrow\Delta CDK=\Delta CAK\left(c.c.c\right)\)
\(\Rightarrowđpcm\)
e)Xét\(\Delta AID-\Delta AHD\)
\(\hept{\begin{cases}AI=AH\\AD.chung\\\widehat{DAI}=\widehat{DAH}\end{cases}}\)
\(\Rightarrow\widehat{AID}=\widehat{AHD}=90^O\)
\(\Rightarrow DI\perp AB.Mà.AC\perp AB\)
\(\Rightarrow DI//AC\)

a) Gọi số đo góc C là x (độ) (0<x<70). => Số đo góc B là x + 40 (độ).
Tổng 3 góc trong 1 tam giác là 180 độ. => Số đo góc A là 180 - (x + 40) - x = 140 - 2x (độ).
AM phân giác góc BAC. => Số đo góc BAM = Số đo góc CAM = (140 - 2x) : 2 = 70 - x (độ).
Tổng 3 góc trong tam giác AMC là 180 độ. => Số đo góc AMC = 180 - Số đo góc CAM - Số đo góc C = 180 - (70 - x) - x = 110 (độ).
Đáp số: Số đo góc AMC = 110 độ.
b) D là trung điểm BC, ED vuông góc với BC. => Tam giác EBC cân tại E. => Số đo góc EBC = Số đo góc ECB = x (độ).
Mà số đo góc ABC là (x + 40) (độ). => Số đo góc ABE = Số đo góc ABC - Số đo góc EBC = (x + 40) - x = 40 (độ).
Đáp số: Số đo góc ABE = 40 độ.
A B C M D E

Bài 1) .
Ta có : AB =AC ( gt)
=> ∆ABC cân tại A
=> B = C
Xét ∆ ABE và ∆ ACD ta có
AD = DE ( gt)
AB = AC ( gt)
B = C ( cmt)
=> ∆ABE = ∆ACD ( c.g.c)
=> EAB = DAC (dpcm)
b) Vì M là trung điểm BC
=> BM = MC
Mà ∆ABC cân tại A ( cmt)
=> AM là trung tuyến ∆ABC
=> AM là trung tuyến đồng thời là đường cao và phân giác ∆ABC
Mà D,E thuộc BC
AM vuông góc với DE
Mà ∆ADE cân tại A ( AD = AE )
=> AM là đường cao đồng thời là phân giác và trung tuyến ∆ ADE
=> AM là phân giác DAE
c) Vì AM là phân giác DAE
=> DAM = EAM = 60/2 = 30 độ
= > Mà AM vuông góc với DE (cmt)
=> AME = AMD = 90 độ
=> AME + MAE + AEM = 180 độ
=> AEM = 180 - 90 - 30 = 60 độ
Mà ∆ADE cân tại A
=> ADE = AED = 60 độ
Bài 2)
Trong ∆ABC có A = 90 độ
=> BAC = 90 độ :))))))

A B C I E D
a) Xét △IAB và △IAD có:
AB = AD (gt)
IAB = IAD (AI: phân giác BAD)
AI: chung
=> △IAB = △IAD (c.g.c)
=> IB = ID (2 cạnh tương ứng)
b) Ta có:
ABI + IBE = 180o (kề bù)
ADI + IDC = 180o (kề bù)
Mà ABI = ADI (△ABI = △ADI)
=> IBE = IDC
Xét △BEI và △DCI có:
IBE = IDC (cmt)
IB = ID (cm câu a)
BIE = DIC (đối đỉnh)
=> △BEI = △DCI (g.c.g)
c) Vì AB = AD (cmt)
=> △ABD cân tại A
=> ABD = \(\frac{180^o-\widehat{BAD}}{2}\) (1)
Ta có:
AE = AB + BE
AC = AD + DC
Mà AB = AD (gt), BE = DC (△BIE = △DIC)
=> AE = AC => △AEC cân tại A
=> AEC = \(\frac{180^o-\widehat{BAD}}{2}\) (2)
Từ (1) và (2) => ABD = AEC
Mà hai góc ở vị trí so le trong => BD // EC
d) Ta có: ABC = 2ACB
Lại có: ABC = BIE + BEI (tính chất góc ngoài)
=> 2ACB = BIE + BEI
=> BIE = DCI
Lại có: DIC = BIE (đối đỉnh) => DIC = DCI => △DIC cân
=> DI = DC
Mà DI = BI => DC = BI
Có: AC = AD + DC
=> AC = AB + IB (đpcm)