Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

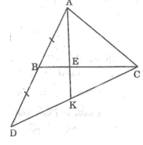
Trong ΔACD ta có:
CB là đường trung tuyến kẻ từ đỉnh C
Mặt khác:
E ∈ BC và BE = 1/3 BC (gt)
Nên: CE = 2/3 CB
Suy ra: E là trọng tâm của ΔACD.
Vì AK đi qua E nên AK là đường trung tuyến của ΔACD
Suy ra K là trung điểm của CD
Vậy KD = KC.

Xét ΔACD có
CB là đường trung tuyến
CE=2/3CB
Do đó: E là trọng tâm của ΔACD
=>AE là đường trung tuyến ứng với cạnh DC
=>K là trung điểm của CD

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

a: Xét ΔADC có
CB là trung tuyến
CE=2/3CB
=>E là trọng tâm
=>K là trung điểm của CD
b: BC+AK=3/2(AE+CE)>3/2AC
a: \(BE+CE=BC\)
=>\(CE+\dfrac{1}{3}BC=BC\)
=>\(EC=\dfrac{2}{3}BC\)
Ta có: BD=BA
mà B nằm giữa D và A
nên B là trung điểm của DA
Xét ΔCAD có
CB là đường trung tuyến
\(CE=\dfrac{2}{3}CB\)
Do đó: E là trọng tâm của ΔCAD
Xét ΔCAD có
E là trọng tâm
AE cắt CD tại K
Do đó: K là trung điểm của CD
=>KC=KD
b: Xét ΔDAC có
E là trọng tâm
DE cắt AC tại M
Do đó: M là trung điểm của AC
=>\(DE=\dfrac{2}{3}DM=\dfrac{2}{3}\cdot9=6\left(cm\right)\)
Ta có DE+EM=DM
=>EM+6=9
=>EM=3(cm)