Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
góc mAB = góc ABC (gt)
Mà 2 góc này nằm ở vị trí so le trong
Nên Am // BC (1)
Chứng minh tương tự ta có:
An // BC (2)
Từ (1) và (2) suy ra Am trùng với An
=> An và Am trùng nhau (đpcm)

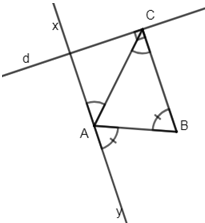
a) Ta có: mà hai góc đó là hai góc so le trong nên
suy ra (1)
mà hai góc đó là hai góc so le trong nên suy ra (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà và
nên suy ra
Mà nên suy ra

a) Vì \(\widehat{AMx}=\widehat{B}\), hai góc này ở vị trí đồng vị nên Mx // BC.
Giả sử Mx không cắt AC. Suy ra Mx // AC. Mx // AC, Mx // BC nên AC // BC(mâu thuẫn với giả thiết ABC là tam giác). Vậy Mx cắt AC
b) Vì \(\widehat{CNy}=\widehat{C}\), hai góc này ở vị trí so le trong nên Ny // BC.
Ny // BC, Mx // BC nên Mx // Ny.

Ta có: `Cx////AB=>` \(\left\{{}\begin{matrix}\widehat{BCx}=\widehat{B}\left(\text{so le trong}\right)\\\widehat{DCx}=\widehat{A}\left(\text{đồng vị}\right)\end{matrix}\right.\)
Mà `\hatA=\hatB` (GT)
`=> \hat(BCx)=\hat(DCx)`
`=> Cx` là phân giác `\hat(DCB)`.
Ta có: \(\widehat{DCx}=\widehat{CAB}\)(hai góc đồng vị, Cx//AB)
\(\widehat{BCx}=\widehat{CBA}\)(hai góc so le trong, Cx//AB)
mà \(\widehat{CAB}=\widehat{CBA}\)
nên \(\widehat{DCx}=\widehat{BCx}\)
hay Cx là tia phân giác của \(\widehat{DCB}\)
Ta có: \(\widehat{MAB}=\widehat{ABC}\)
mà hai góc này ở vị trí so le trong
nên AM//BC
Ta có: \(\widehat{NAC}=\widehat{ABC}\)
mà hai góc này ở vị trí so le trong
nên AN//BC
Ta có: AM//BC
AN//BC
AM,AN có điểm chung là A
Do đó: M,A,N thẳng hàng
hay AM và AN là hai tia đối nhau