Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Giả sử điểm K thỏa mãn:
\(\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{CB}\)\(\Leftrightarrow\overrightarrow{KB}+\overrightarrow{BA}+2\overrightarrow{KB}=\overrightarrow{CB}\)
\(\Leftrightarrow3\overrightarrow{KB}=\overrightarrow{CB}-\overrightarrow{BA}\)
\(\Leftrightarrow\overrightarrow{KB}=\overrightarrow{CB}+\overrightarrow{AB}\).
Xác định: \(\overrightarrow{CB}+\overrightarrow{AB}\).
A B C D
Lấy điểm D sao cho B là trung điểm của DC.
\(\overrightarrow{CB}+\overrightarrow{AB}=\overrightarrow{BD}+\overrightarrow{AB}=\overrightarrow{AD}\).
Điểm K xác định sao cho : \(\overrightarrow{KB}=\overrightarrow{AD}\) hay tứ giác AKBD là hình bình hành.
A B C D K
b) Gọi G là trọng tâm tam giác ABC.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+2\overrightarrow{MG}\)\(+2\overrightarrow{GC}\)
\(=4\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+\overrightarrow{GC}\)
\(=4\overrightarrow{MG}+\overrightarrow{GC}\).
Giả sử điểm M thỏa mãn:
\(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow4\overrightarrow{MG}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MG}=\dfrac{\overrightarrow{CG}}{4}\).
Điểm M được xác định để \(\overrightarrow{MG}=\dfrac{\overrightarrow{CG}}{4}\).
A B C G T M
Gọi T là trung điểm của AB nên \(\overrightarrow{CG}=2\overrightarrow{GT}\).
Vì vậy điểm M được xác định là trung điểm của GT.
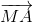 +
+ = 2
= 2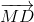
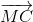 =
= 
Gọi N là trung điểm AB
\(2\overrightarrow{AM}+\overrightarrow{MC}+\overrightarrow{BM}=\overrightarrow{CA}\)
\(\Leftrightarrow2\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow{CA}\)
\(\Leftrightarrow2\overrightarrow{AM}=\overrightarrow{CA}+\overrightarrow{CB}\)
\(\Leftrightarrow2\overrightarrow{AM}=2\overrightarrow{CN}\)
\(\Rightarrow\overrightarrow{AM}=\overrightarrow{CN}\)
\(\Rightarrow M\) là đỉnh thứ tư của hình bình hành ACNM