Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) đặc C (x;y) , ta có : C \(\in\) (d) \(\Leftrightarrow x=-2y-1\)
vậy C (-2y -1 ; y ).
tam giác ABC cân tại C khi và chỉ khi
CA = CB \(\Leftrightarrow\) CA2 = CB2
\(\Leftrightarrow\) (3+ 2y + 1)2 + (- 1- y)2 = (- 1+ 2y + 1)2 + (- 2- y)2
\(\Leftrightarrow\) (4 + 2y)2 + (1 + y)2 = 4y2 + (2 + y)2
giải ra ta được y = \(\dfrac{-13}{14}\) ; x = \(-2\left(\dfrac{-13}{14}\right)-1=\dfrac{13}{7}-1=\dfrac{6}{7}\)
vậy C có tọa độ là \(\left(\dfrac{6}{7};\dfrac{-13}{14}\right)\)
b) xét điểm M (- 2t - 1 ; t) trên (d) , ta có :
\(\widehat{AMB}\) = 900 \(\Leftrightarrow\) AM2 + BM2 = AB2
\(\Leftrightarrow\) (4 + 2t)2 + (1 + t)2 + 4t2 + (2 + t)2 = 17
\(\Leftrightarrow\) 10t2 +22t + 4 = 0 \(\Leftrightarrow\) 5t2 + 11t + 2 = 0
\(\Leftrightarrow\left\{{}\begin{matrix}t=\dfrac{-1}{5}\\t=-2\end{matrix}\right.\)
vậy có 2 điểm thỏa mãn đề bài là M1\(\left(\dfrac{-3}{5};\dfrac{-1}{5}\right)\) và M2\(\left(3;-2\right)\)

a)Giả sử điểm K thỏa mãn:
\(\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{CB}\)\(\Leftrightarrow\overrightarrow{KB}+\overrightarrow{BA}+2\overrightarrow{KB}=\overrightarrow{CB}\)
\(\Leftrightarrow3\overrightarrow{KB}=\overrightarrow{CB}-\overrightarrow{BA}\)
\(\Leftrightarrow\overrightarrow{KB}=\overrightarrow{CB}+\overrightarrow{AB}\).
Xác định: \(\overrightarrow{CB}+\overrightarrow{AB}\).
A B C D
Lấy điểm D sao cho B là trung điểm của DC.
\(\overrightarrow{CB}+\overrightarrow{AB}=\overrightarrow{BD}+\overrightarrow{AB}=\overrightarrow{AD}\).
Điểm K xác định sao cho : \(\overrightarrow{KB}=\overrightarrow{AD}\) hay tứ giác AKBD là hình bình hành.
A B C D K
b) Gọi G là trọng tâm tam giác ABC.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+2\overrightarrow{MG}\)\(+2\overrightarrow{GC}\)
\(=4\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+\overrightarrow{GC}\)
\(=4\overrightarrow{MG}+\overrightarrow{GC}\).
Giả sử điểm M thỏa mãn:
\(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow4\overrightarrow{MG}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MG}=\dfrac{\overrightarrow{CG}}{4}\).
Điểm M được xác định để \(\overrightarrow{MG}=\dfrac{\overrightarrow{CG}}{4}\).
A B C G T M
Gọi T là trung điểm của AB nên \(\overrightarrow{CG}=2\overrightarrow{GT}\).
Vì vậy điểm M được xác định là trung điểm của GT.

a) Từ điểm I trên AB thỏa mãn IA = 1/2 IB ta vẽ đường song song với BC. Điểm N nằm trên đó.
B) tương tự câu a)

Kí hiệu v là vectơ nhé
1) Gọi I là điểm thỏa v IA + v IB + 3 v IC = 0 (1) (đây là vectơ 0 nhé)
=> v IA + v IA + v AB + 3 v IA + 3 AC = 0
=> 5 v IA = - (v AB + 3 v AC) => I cố định (do A, B, C cố định)
Ta có: v a = v MA + v MB + 3 v MC = v MI + v IA + v MI + v IB + 3 v MI + 3 v IB =
= 5 v MI + ( v IA + v IB + 3 v IC) = 5 v MI (do (1))
=> | v a| = | 5 v MI| = 5 MI
|v a| Min <=> MI min <=> MI = 0 <=> M trùng I
Vậy khi M là điểm thỏa 5 v MA = - (v AB + 3 v AC) (cố định) thì độ dài vectơ a nhỏ nhất.
Với mọi điểm O ta có :
\(\overrightarrow{u}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{2MC}=\overrightarrow{OA}-\overrightarrow{OM}+\overrightarrow{OB}-\overrightarrow{OM}+2\left(\overrightarrow{OC}-\overrightarrow{OM}\right)\)
\(=\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}-4\overrightarrow{OM}\)
Ta chọn điểm O sao cho \(\overrightarrow{v}=\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow{0}\)
( Chú ý: Nếu G là trọng tâm tam giác ABC thì \(\overrightarrow{v}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OC}=3\overrightarrow{OG}+\overrightarrow{OC}=4\overrightarrow{OG}+\overrightarrow{GC}\). Bởi vậy để \(\overrightarrow{v}=\overrightarrow{0}\)ta chọn điểm O sao cho \(\overrightarrow{GO}=\frac{1}{4}\overrightarrow{GC}\))
Khi đó \(\overrightarrow{u}=-4\overrightarrow{OM}\)và do đó \(|\overrightarrow{u}|=4OM\)
Độ dài vectơ \(\overrightarrow{u}\)nhỏ nhất khi và chỉ khi 4OM nhỏ nhất hay M là hình chiếu vuông góc của O trên d

a) \(x_G=\dfrac{-3+9+\left(-5\right)}{3}=\dfrac{1}{3}\).
\(y_G=\dfrac{6+\left(-10\right)+4}{3}=0\).
Vậy \(G\left(\dfrac{1}{3};0\right)\).
b) Tứ giác BGCD là hình bình hành khi và chỉ khi:
\(\overrightarrow{BG}=\overrightarrow{CD}\).
Gọi \(D\left(x;y\right)\).
\(\overrightarrow{BG}\left(-\dfrac{26}{3};10\right);\overrightarrow{CD}\left(x+5;y-4\right)\).
Do \(\overrightarrow{BG}=\overrightarrow{CD}\) nên \(\left\{{}\begin{matrix}x+5=-\dfrac{26}{3}\\y-4=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{41}{3}\\y=14\end{matrix}\right.\).
Vậy \(D\left(-\dfrac{41}{3};14\right)\).
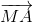 +
+ = 2
= 2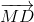
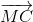 =
= 


Gọi D là trung điểm của cạnh AB, ta có:
Đẳng thức đã cho trở thành:
2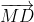 + 2
+ 2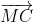 =
= 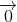
=>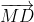 +
+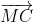 =
= 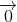
Đẳng thức này chứng tỏ M là trung điểm của CD