Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BEDF có
DF//BE
ED//BF
Do đó: BEDF là hình bình hành
mà BD là đường phân giác
nên BEDF là hình thoi
Suy ra: DB là tia phân giác của góc EDF
b: Ta có: ED//BC
nên \(\widehat{AED}=\widehat{ABC};\widehat{ADE}=\widehat{ACB}\)

A B C D x y F E
a) Ta có:góc EDB= góc FBD(ED//BF)
góc FDB= góc EBD(DF//BE)
Mà góc FBD = góc EBD (BD là tia phân giác góc EBF)
=>góc EDB= góc FDB
=>DB là tia phân giác góc EDF
b)Vì ED//BC
=>góc AED=góc ABC(2 góc đồng vị)
Vì DF//AB
=>góc ADE= góc ACB(2 góc đồng vị)
Vậy góc AED=góc ABC; góc ADE =góc ACB
c)Xét tam giác EBD và tam giác FDB có:
góc BDE= góc DBF
BD chung
góc EDB= góc FBD
=>tam giác EBD=tam giác FDB(g-c-g)
=>góc BED = góc BFD

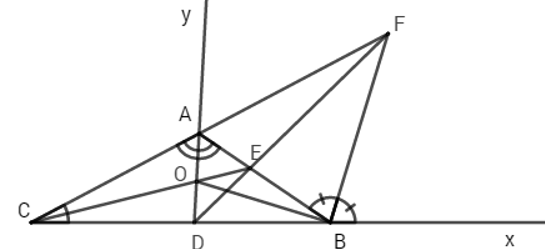
a) Xét \(\Delta ABC\) có tia phân giác \(BAC,ACB\) cắt nhau tại O suy ra O là giao điểm của 3 đường phân giác trong tam giác ABC suy ra BO là phân giác của \(\widehat{CBA}\) (tính chất 3 đường phân giác của tam giác)
\(\Rightarrow DBO=ABO=\dfrac{DBA}{2}\left(1\right)\) ( tính chất tia phân giác )
Lại có BF là phân giác của \(\widehat{ABx\left(gt\right)}\) \(=ABF=FBx\left(2\right)\)
( tính chất của tia phân giác )
Mà \(ABD+ABx=180^o\left(3\right)\left(kềbu\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow OBA+ABF=180^o\div2=90^o\Rightarrow BO\text{⊥ }BF\)
b) Ta có \(FAB+BAC=180^o\)( kề bù ) mà \(BAC=120^o\left(gt\right)\Rightarrow FAB=60^o\)
\(\Rightarrow\text{AD là phân giác của}\widehat{BAC}\) ( dấu hiệu nhận biết tia phân giác )
\(\Rightarrow BAD=CAD=60^o\) ( tính chất tia phân giác )
\(\Rightarrow FAy=CAD=60^o\) ( đối đỉnh ) \(\Rightarrow FAB=FAy=60^o\Rightarrow\) AF là tia phân giác của \(BAy\) ( dấu hiệu nhận biết tia phân giác )
Vậy \(\Delta ABD\) có hai tia phân giác của hai góc ngoài tại đỉnh A và đỉnh B cắt nhau tại F nên suy ra DF là phân giác của \(ADB=BDF=ADF\) ( tính chất tia phân giác )
c) Xét \(\Delta ACD\) có phân giác góc ngoài tại đỉnh A và phân giác trong tại đỉnh C cắt nhau tại E nên suy ra DE cũng là phân giác của \(ADB\Rightarrow\)\(D,E,F\) thẳng hàng
thật là ngược mộ nha
dù không biết đúng hay sai nhưng lâu lắm mới thấy người làm nguyên một bài toán hình thế này mà còn có hình nữa![]()


cùi . đéo giải được bài lớp 6 của tao.
A B C D F E y x
mk chỉ bt vẽ hình thui cn c/m mk chưa hc đến phần này ms hc từ vuông góc đến song song thui thông cảm