K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TV
1
DT
0

NT
0


AH
Akai Haruma
Giáo viên
30 tháng 6 2019
Lời giải:
Theo công thức lượng giác, ta có:
Xét tam giác $AIC$ vuông tại $I$:\(\cos A=\frac{AI}{AC}\)
Xét tam giác $ABH$ vuông tại $H$: \(\cos B=\frac{BH}{AB}\)
Xét tam giác $BKC$ vuông tại $K$: \(\cos C=\frac{CK}{CB}\)
Từ những điều trên suy ra:
\(\cos A.\cos B.\cos C=\frac{AI}{AC}.\frac{BH}{AB}.\frac{CK}{CB}\)
\(\Rightarrow AI.BH.CK=AB.BC.AC.\cos A.\cos B.\cos C\) (đpcm)

27 tháng 12 2016
bc(b2-c2)cosA+ca(c2-a2)cosB+ba(a2-b2)cosC
\(\frac{\left(b^2-c^2\right)\left(b^2+c^2-a^2\right)}{2}+\frac{\left(c^2-a^2\right)\left(c^2+a^2-b^2\right)}{2}+\frac{\left(a^2-b^2\right)\left(a^2+b^2-c^2\right)}{2}\)
Giờ nhân mấy cái đấy vô rồi rút gọn là nó bằng 0 đó



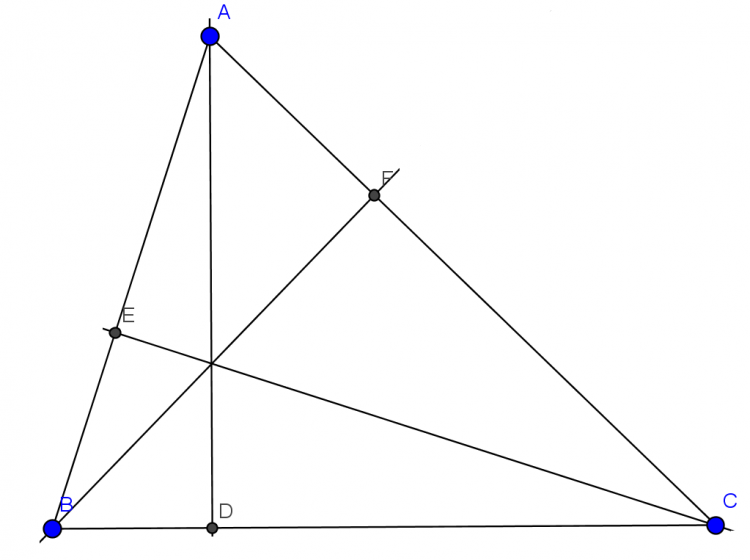


Xét tam giác ABC nhọn có \(BC^2=AB^2+AC^2-2AB\cdot AC\cdot\cos\widehat{A}\)
\(\Rightarrow\cos\widehat{A}=\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4\cdot\dfrac{1}{2}AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4S_{ABC}}\)
Cmtt: \(\left\{{}\begin{matrix}\cos\widehat{B}=\dfrac{AB^2+BC^2-AC^2}{4S_{ABC}}\\\cos\widehat{C}=\dfrac{AC^2+BC^2-AB^2}{4S_{ABC}}\end{matrix}\right.\)
\(\Rightarrow\cos\widehat{A}+\cos\widehat{B}+\cos\widehat{C}\\ =\dfrac{AB^2+AC^2-BC^2+AB^2+BC^2-AC^2+AC^2+BC^2-AB^2}{4S_{ABC}}\\ =\dfrac{AB^2+AC^2+BC62}{4S_{ABC}}\)