Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hỏi viết mấy cái kiểu thập phân, kí hiệu kiểu nào vậy bạn @@!
Bài này mình cũng tạm biết biết :V
À giờ mình thấy nó hơi hại não, cho mình rút lui câu trước nah :V
Mình cũng cũng ngu toán chứ bộ T_T

a: Xet tứ giác ABCD có
N là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AD=BC
b: Xét tứ giác ACBE có
M là trung điểm chung của AB và CE
=>ACBE là hình bình hành
=>AE//BC

a) Xét tam giác ANM và tam giác CNP có:
AN=CN( vì N là trung điểm của AC)
góc ANM= góc CNP ( đối đỉnh)
NM=NP
=> tam giác ANM=tam giác CNP ( c.g.c)
=> góc A= góc NCP
mà chúng là 2 góc so le trong => CP//AB
b) theo a) tam giác ANM=tam giác CNP
=> AM=CP
Mà AM= MB ( vì M là trung điểm của AB)
=> CP=MB
c) Vì M là trung điểm của AB, N là trung điểm của AC => MN là đường trung bình của tam giác ABC
=> BC=2MN
a) - Xét tam giác CPN và tam giác AMN có:
MN=NP (gt)
Góc ANM=CNP (2 góc đối đỉnh)
AN=NC (gt)
Do đó: tam giác ANM= tam giác CNP (c.g.c)
- Vì tam giác ANM= tam giác CNP nên góc ANM = góc CNP ( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong nên AB//CP
b) Vì tam giác ANM= tam giác CNP( cmt) nên AM =CP (2 cạnh tương ứng)
Mà AM=MB (vì điểm M là trung điểm của AB) nên CP= MB
c) - Ta có: CP= AB ( câu a)
=> Góc BMC= góc MCP (2 góc so le trong)
- Xét tam giác MBC và tam giác CPM có:
MB=PC ( câu b)
MC là cạnh chung
Góc BMC =góc MCD (cmt)
Do đó: tam giác MBC= tam giác CPM (c.g.c)
=> PM= BC ( 2 cạnh tương ứng)
Mà MN= NP hay MP= 2MN
Vậy BC=2MN

a/ Xét \(\Delta ANM\)và \(\Delta CND\)có :
+) \(MN=ND\left(gt\right).\)
+) \(AN=NC.\)
+) Góc \(ANM\)= Góc \(NCD.\)
\(\Rightarrow\Delta ANM=\Delta CND\left(c.g.c\right).\)
\(\Rightarrow CD=AM.\)
Mà \(AM=BM.\)
\(\Rightarrow CD=BM.\)
b/ Xét \(\Delta ABC\)có \(M,N\)lần lượt là trung điểm của \(AB,AC.\)
\(\Rightarrow MN\)là đường trung bình của \(\Delta ABC.\)
\(\Rightarrow MN//BC\)và \(MN=\frac{1}{2}BC.\)
c/ Ta có \(MN=\frac{1}{2}BC.\)
\(\Rightarrow2MN=BC.\)
\(\Leftrightarrow MD=BC.\)
Xét tứ giác \(BMDC\)có \(MD=BC\)và \(MD//BC.\)
\(\Rightarrow\)Tứ giác \(BMDC\)là hình bình hành.
\(\Rightarrow MC\)và \(BD\)là hai đường chéo của hình bình hành \(BMDC.\)
\(\Rightarrow BD\)đi qua trung điểm của đoạn thẳng \(MC.\)
#Riin

tự kẻ hình nha
a) xét tam giác AMN và tam gáic CEN có
AN=NC(gt)
MN=NE(gt)
ANM=CNE( đối đỉnh)
=> tam giác AMN= tam giác CEN(cgc)
=> AM=CE(hai cạnh tương ứng) mà AM=MB=> MB=CE
=> CEN=AMN(hai góc tương ứng)
mà CEN so le trong với AMN mà A,M,B thẳng hàng=> MB//CE
c) từ MB//CE=> BMC=MCE( so le trong)
xét tam giác BMC và tam gíac ECM có
MC chung
BMC=MCE(cmt)
MB=CE(cmt)
=> tam gíac BMC= tam giác ECM(ccg)
d) từ tam giác BMC= tam giác CEM=> BCM=EMC( hai góc tương ứng), ME=BC( hai cạnh tương ứng)
mà BCM so le trong với EMC=> MN//BC
vì MN=NE mà ME=BC(cmt)
=> BC=2MN=> MN=1/2BC

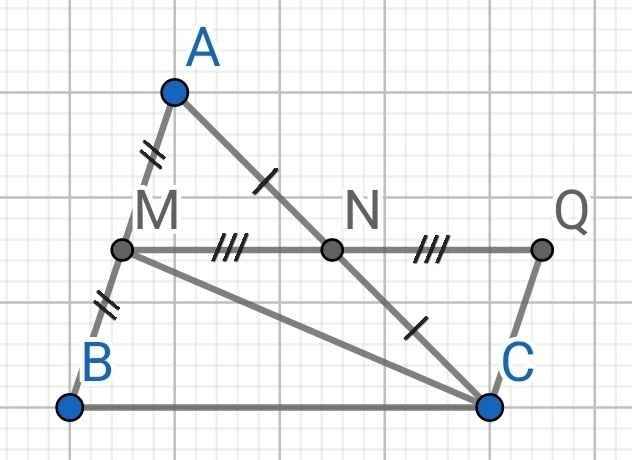
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC
a/ Xét \(\Delta ANM\) và \(\Delta CND\) có
NA=NC (gt); NM=ND (gt)
\(\widehat{ANM}=\widehat{CND}\) (góc đối đỉnh)
\(\Rightarrow\Delta ANM=\Delta CND\left(c.g.c\right)\)
b/
\(\Delta ANM=\Delta CND\left(cmt\right)\Rightarrow\widehat{BAC}=\widehat{ACD}\) => AB//CD (hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong băng nhau thì hai đường thẳng đó // với nhau)
c/
Ta có
MA=MB (gt); NA=NC (gt) -> MN là đường trung bình của tg ABC => MN=1/2 BC (đường trung bình của tg thì // và =1/2 cạnh đáy)
lớp 7 chưa học đường trung bình đâu b :D
( hình vẽ riêng vào tcn xem)
a) Xét tam giác ANM và tam giác CND có:
DN=NM ( gt)
^ANM=^CND (đối đỉnh)
AN=CN ( N trung điểm AC)
=>tam giác ANM = tam giác CND (c.g.c) (đpcm)
b) Vì tam giác ANM = tam giác CND (c.g.c) (cmt)
=> ^AMN=^NDC ( 2 góc so le)
=> AM//DC
Mà AM=MB ( M trung đ AB)
=> AB//DC (đpcm)
c) Nối C và M lại với nhau
vì tam giác ANM=tam giác CND (c.g.c) ) (cmt)
=> AM=CD ( 2 cạnh tương ứng)
Mà AM=MB ( gt)
=> MB=CD
Xét tam giác CMD và tam giác MCB có:
MB=CD (cmt)
^MCB=^DMC ( DC//AB (cmt) )
CM chung
=> tam giác CMD =tam giác MCB (c.g.c)
=> DM=CB ( hai cạnh tương ứng)
Lại có: N trung điểm DM
=> DN=NM=1/2DM
Do đó: NM=1/2CB (đpcm)