Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B và D giống nhau nên chắc chắn cả 2 đều đúng
Kiểm tra 2 đáp án A và C:
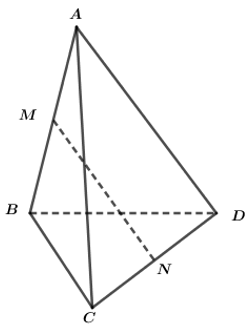
\(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{MC}+\overrightarrow{MD}\right)=\frac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{MB}+\overrightarrow{BD}\right)=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{BD}\right)\)
Vậy đáp án A đúng nên đáp án C sai

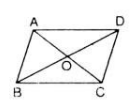
Ta có vecto MM' + vecto MA = vecto MB
=> MM'BA là hình bình hành
vì A , B cố định => vecto AB cố định
xét phép tịnh tiến qua vecto AB biến M => M'
=> vecto MM' = vecto AB
=> M' là ảnh của M
Mặt khác điểm M chạy trên đường tròn (O) nên M' sẽ chạy trên đường tròn (O') là ảnh của
(O) thông qua phép tịnh tiến vecto AB
Vậy quỹ tích M' là đường tròn (O')

ta có : \(\overrightarrow{MM'}+\overrightarrow{MA}=\overrightarrow{MB}\Leftrightarrow\overrightarrow{MM'}=\overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{AB}\)
mà \(M\in\left(O\right)\Rightarrow M'\in\left(O'\right)\) với \(\left(O'\right)=T_{\overrightarrow{AB}}\left(O\right)\)
vậy tập hợp điểm \(M\) là đường tròn \(\left(O'\right)\) với \(\left(O'\right)\) là ảnh của đường tròn \(\left(O\right)\) qua \(T_{\overrightarrow{AB}}\)




tại sao lại nhân 2 vô nơi(2) vậy bạn