Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tự vẽ hình nhé
CM tam giác ABC= tam giác AEG
\(\Rightarrow\)góc GEA= góc ABC
góc EGA = góc ACB
ta có góc HAC= góc ABH ( cùng phụ goc BAH)
góc OAE= góc HAC
\(\Rightarrow\) góc OEA= góc OAE
\(\Rightarrow\)OA=OE
CMTT: OA=OG
suy ra OE=OG (1)
ta có góc GAC+ HAC+BAH=180độ
mà BAH=OAG
 \(\Rightarrow\) OAG+GAC+HAC=180 độ
O,A ,H thẳng hàng(2)
từ 1 va 2 suy ra đfcm
O là trung điểm EG

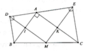
A B C M D E F K
a) Các tam giác DBA và tam giác EAC vuông cân nên \(\widehat{ABD}=\widehat{DAB}=45^o,\widehat{CAE}=\widehat{ECA}=45^o\).
\(\widehat{DAE}=\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=45^o+90^o+45^o=180^o\).
Suy ra D, A, E thẳng hàng.
b) Có M là trung điểm của BC và tam giác BAC vuông tại A nên MA = MB = MC.
Suy ra \(\Delta DBM=\Delta DAM\left(c.c.c\right)\). Vì vậy \(\widehat{BDM}=\widehat{ADM}\) hay DM là tia phân giác góc ADB.
mà tam giác BDA cân tại D nên DM cũng là đường cao hay \(DM\perp AB\).
Tương tự cho \(EM\perp AC\).
c) Theo chứng minh trên DM là tia phân giá góc ADB nên \(\widehat{BDM}=\widehat{MDA}=45^o\). Tương tự \(\widehat{AEK}=\widehat{KEC}=45^o\).
Vì vậy ta, giác DME vuông cân.
d) Do các tam giác ADB và tam giác AEC cân và DF và EK là đường cao tương ứng nên DF và EK cũng là các đường trung tuyến.
Vì vậy F và K lần lượt là trung điểm của AB và AC.
Từ đó suy ra FK là đường trung bình của tam giác BAC hay \(FK=\frac{1}{2}BC\).

Câu hỏi của Bảo Châu Trần - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo lời giải tại đây nhé.
Bài 5:
Cho ABC vuông tại A, kẻ phân giác BM ( M AC), trên cạnh BC
lấy điểm E sao cho BE = AB
a) Chứng minh 2 tam giác BAM BEM .
b) Gọi F là giao điểm của đường thẳng ME và đường thẳng AB.
Chứng minh: FM = MC.
c) Chứng minh: AM < MC
d) Chứng minh AE // FC.


a) Ta thấy ngay \(\Delta ABE=\Delta ACD\) (Hai cạnh góc vuông)
b) Do \(\Delta ABE=\Delta ACD\Rightarrow\widehat{ABE}=\widehat{ACD}\)
mà \(\widehat{ABE}=\widehat{MAC}\) (Cùng phụ với góc BEA)
\(\Rightarrow\widehat{MAC}=\widehat{MCA}\) hay tam giác MAC cân tại M.
c) Xét tam giác vuông ADC: \(\widehat{MCA}=\widehat{MAC}\Rightarrow\widehat{MDA}=\widehat{MAD}\Rightarrow MD=MA\)
Vậy thì DM = MA = MC hay M là trung điểm DC.
Xét tam giácAIC có M là trung điểm DC, MK // DI nên MK là đường trung bình tam giác DIC.
Suy ra K là trung điểm IC.
d) Xét tam giác DIC có IM và DK là hai trung tuyến nên G là trọng tâm tam giác.
Gọi N là giao điểm của CG với DE thì DN = NI.
Áp dụng định lý Talet ta có:
\(\frac{MF}{DN}=\frac{CF}{CN}=\frac{FK}{NI}\)
Mà DN = NI nên MF = FK.

a) Chứng minh D E A ^ = 180 0
b) Chứng minh
A I M ^ = A K M ^ = I A K ^ = 90 0
c) Chứng minh DDME có E D M ^ = D E M ^ = 45 0
Þ DDME vuông cân ở M.

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Vì FA = EC
BD = DC
=> DE là đường trung bình ∆ABC
=> ED = \(\frac{1}{2}\)AB = FA
Mà FA = FK
=> ED = FK
Vì FA = FB
BD = DC
=> FD là đường trung bình ∆ABC
=> FD = \(\frac{1}{2}\)AC = AE
Mà AE =EG
FD = EG
=> AE = FD
Ta có : CED = DFB = EDF ( so le trong)
=> KFD = DEG
Xét ∆KFD và ∆DEG ta có :
KF = DE (cmt)
FD = EG
KFD = DEG
=> ∆KFD = ∆DEG (c.g.c)
=> KD = DG
=> FKD = EDG
=> FDK = EGD
Mà EDG + EGD + DEC + GEC = 180°
=> EDG + EGD + DEC = 90°
=> EDG + FDK + EDF = 90°
=> GDK = 90°
Vì DK = DG
=> ∆DGK cân tại D
=> GDK = 90°
=> ∆DGK vuông cân tại D