Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\Delta ABC\)là tam giác đều
\(\Rightarrow\)\(\widehat{ABC}=\widehat{ACB}=\widehat{BAC}=60^0\)
\(\Delta AMN\)cân tại \(A\)do \(AM=AN\)(gt)
mà \(\widehat{MAN}=60^0\)
nên \(\Delta AMN\)là tam giác đều
b) \(\Delta AMN\)là tam giác đều
\(\Rightarrow\)\(\widehat{AMN}=60^0\)
\(\Rightarrow\)\(\widehat{AMN}=\widehat{ABC}\left(=60^0\right)\)
mà \(\widehat{AMN}\)và \(\widehat{ABC}\)đồng vị
\(\Rightarrow\)\(MN//BC\)

A B C M N = =
a) Ta có:
AM + MB = AB
AN + NC = AC
Mà AB = AC(△ABC cân) và AM = AN (gt)
=> MB = NC
Xét △MBC và △NCB có:
MB = NC (cmt)
MBC = NCB (△ABC cân)
BC: chung
=> △MBC = △NCB (c.g.c)
=> BN = CM (2 cạnh tương ứng)
b) Vì △MBC = △NCB
=> MCB = NBC (2 góc tương ứng)
=> △BOC cân
c) Vì AM = AN (gt)
=> △AMN cân tại A
=> AMN = \(\frac{180^o-A}{2}\)(1)
Vì △ABC cân tại A
=> ABC = \(\frac{180^o-A}{2}\)(2)
Từ (1) và (2) => AMN = ABC
Mà hai góc AMN và ABC ở vị trí đồng vị
=> MN // BC

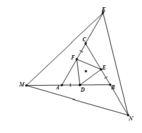
TG ABC đều =>AB=AC=BC=>AM+MB=BN+NC=CZ+ZA
Mà AM=BN=CZ=>BM=NC=AZ
Xét Tg AMZ và tg CZN, có:
Góc A= góc C( Tg ABC đều)
AM=CZ
AZ=CN
Vậy tg AMZ= tg CZN(c.g.c)
=> MZ=NZ( cạnh tương ứng)(1)
Tương tự ta có: MZ=MN(2)
Từ (1), (2)=> MZ=ZN=NM=> tg MNZ đều
Cau hoi tuong tu nha bn !