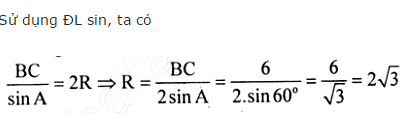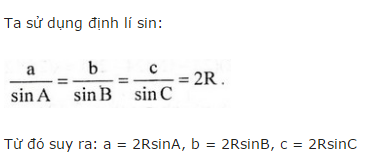K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
SG
1

AT
Anh Triêt
30 tháng 3 2017
Đúng(0)
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
22 tháng 12 2017
Áp dụng định lý Sin trong tam giác ABC ta có:
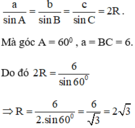
Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.