Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
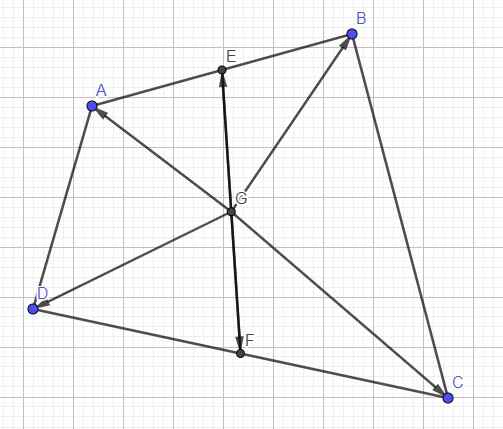
E và F là trung điểm AB và CD nên: \(\overrightarrow{AB}=2\overrightarrow{AE}\) ; \(\overrightarrow{DC}=2\overrightarrow{DF}\)
G là trung điểm EF nên: \(\overrightarrow{AE}+\overrightarrow{AF}=2\overrightarrow{AG}\)
Do đó:
\(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AE}+\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{AD}=2\overrightarrow{AE}+2\overrightarrow{AD}+2\overrightarrow{DF}\)
\(=2\overrightarrow{AE}+2\left(\overrightarrow{AD}+\overrightarrow{DF}\right)=2\overrightarrow{AE}+2\overrightarrow{AF}=2\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=4\overrightarrow{AG}\)
b.
\(\left(\overrightarrow{GA}+\overrightarrow{GB}\right)+\left(\overrightarrow{GC}+\overrightarrow{GD}\right)=2\overrightarrow{GE}+2\overrightarrow{GF}=2\left(\overrightarrow{GE}+\overrightarrow{GF}\right)=2.\overrightarrow{0}=\overrightarrow{0}\)
c.
Từ câu b ta có:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{GO}+\overrightarrow{OA}+\overrightarrow{OG}+\overrightarrow{OB}+\overrightarrow{GO}+\overrightarrow{OC}+\overrightarrow{GO}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{GO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\)
\(\Rightarrow\overrightarrow{OG}=\dfrac{1}{4}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)\)

\(\overrightarrow{KA}=-\overrightarrow{AK}=-\frac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=-\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right)\)
\(=-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\)
\(\overrightarrow{KD}=\overrightarrow{AD}-\overrightarrow{AK}=\overrightarrow{AD}+\overrightarrow{KA}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\)
\(=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\)

a: \(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}\)
\(=\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\overrightarrow{BA}-\dfrac{1}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)

Lời giải:
Vì $M,N$ lần lượt là trung điểm của $AB,AC$ nên $MN$ là đường trung bình ứng với cạnh $BC$ của tam giác $ABC$
$\Rightarrow MN\parallel BC$ và $MN=\frac{1}{2}BC$
$\Rightarrow \overrightarrow{MN}=\frac{1}{2}\overrightarrow{BC}$
Mà:
$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}$ do $P$ là trung điểm $BC$
Do đó: $\overrightarrow{MN}=\overrightarrow{BP}$
---------------------------
Dễ chứng minh $NP$ là đường trung bình ứng với cạnh $AB$
$\Rightarrow \overrightarrow{PN}=\frac{1}{2}\overrightarrow{BA}$
Mà $M$ là trung điểm $AB$ nên $\overrightarrow{MA}=\frac{1}{2}\overrightarrow{BA}$
Vậy: $\overrightarrow{MA}=\overrightarrow{PN}$
a:Sửa đề: K nằm trên AC sao cho AK=1/3AC
\(\overrightarrow{BI}=\overrightarrow{BM}+\overrightarrow{MI}\)
\(=\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{MA}\)
\(=\dfrac{1}{2}\overrightarrow{BC}-\dfrac{1}{2}\cdot\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AC}\)
\(=-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
b: Gọi E là trung điểm của CK
=>AK=KE=CE
Xét ΔAME có AI/AM=AK/AE
nên IK//ME
Xét ΔBKC có CM/CB=CE/CK
nên ME//BK
IK//ME
ME//BK
Do đó: B,I,K thẳng hàng