Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đo các góc A,B,C lần lượt là :a,b,c
Theo đề bài ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)và a+b+c=180*
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{180^o}{15}=12\)
\(\frac{a}{3}=12\Rightarrow a=12.3=36\)
\(\frac{b}{5}=12\Rightarrow12.5=60\)
\(\frac{c}{7}=12\Rightarrow12.7=84\)
Vậy số đo các góc A,B,C lần lượt là:36 ;60 ;84

Giải
a) Xét \(\Delta ABC\) ta có :
\(\widehat{B}=\widehat{A}+\widehat{C}=180^0\) ( Định lí tổng 3 góc của 1 tam giác )
\(\widehat{B}=90^0+32^0=180^0\)
\(\widehat{B}=122^0=180^0\)
\(\widehat{B}=180^0-122^0=58^0\)
b)
Theo bài ra ta có : \(\widehat{A}:\widehat{B}:\widehat{C}=2:7:1\)
\(\Rightarrow\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{7}=\dfrac{\widehat{C}}{1}\)
Lại có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( Định lí tổng 3 góc của 1 tam giác )
Áp dụng tính chất của dãy tỉ số bằng nhau nên ta có :
\(\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{7}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{2+7+1}=\dfrac{180^0}{10}=18^0\)
\(+)\)\(\dfrac{\widehat{A}}{2}=18^0\Rightarrow\widehat{A}=18^0\times2=36^0\)
\(+)\)\(\dfrac{\widehat{B}}{7}=18^0\Rightarrow\widehat{B}=18^0\times7=126^0\)
\(+)\)\(\dfrac{\widehat{C}}{1}=18^0\Rightarrow\widehat{C}=18^0\times1=18^0\)
c)
Xét \(\Delta ABC\) ta có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( Định lí trong 3 góc cùng 1 tam giác )
\(\widehat{A}+75^0+\widehat{C}=180^0\)
\(\widehat{A}+\widehat{C}=180^0-75^0\)
\(\widehat{A}+\widehat{C}=105^0\)
Theo bài ra ta có :
\(\widehat{A}:\widehat{C}=3:2\Rightarrow\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau nên ta có :
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{C}}{2}=\dfrac{\widehat{A}+\widehat{C}}{3+2}=\dfrac{105^0}{5}=21^0\)
\(+)\)\(\dfrac{\widehat{A}}{3}=21^0\Rightarrow\widehat{A}=21^0\times3=63^0\)
\(+)\)\(\dfrac{\widehat{C}}{2}=21^0\Rightarrow\widehat{C}=21^0\times2=42^0\)

a.
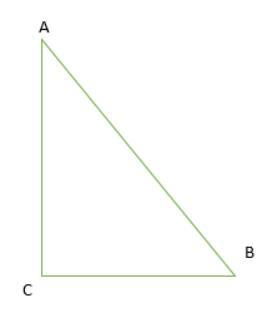
Góc CAB có số đo là 40 độ
Góc ABC có số đo là 50 độ
Góc ACB có số đo là 90 độ
b. Tổng ba góc trong tam giác là: 180 độ bằng với kết quả của các bạn khác.

Ta có : tổng các góc = 180 o
Tổng số phần của các góc là :
2 + 3 + 4 = 9 phần
Số đo của góc thứ nhất là :
\(180:9\times2=40^o\)
Số đo của góc thứ 2 là :
\(180:9\times3=60\)
Số đo của góc thứ 3 là :
\(180:9\times4=80^o\)
Đáp số : .................

Tia BD nằm giữa hai tia BA và BC nên
∠ABC = ∠ADB + ∠DBC ; ∠DBC =∠ABC - ∠ADB
∠DBC = 55 0 - 30 0 = 25 0
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có∠ABx = ∠DBx - ∠DBA= 90 0 - 30 0 = 60 0
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có ∠ABx = ∠DBx + ∠DBA= 90 0 + 30 0 = 120 0

Tia BD nằm giữa hai tia BA và BC nên
A B C ^ = A D B ^ + D B C ^ ; D B C ^ = A B C ^ - A D B ^
D B C ^ = 55 ° - 30 ° = 25 °
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có A B x ^ = D B x ^ - D B A ^ = 90 ° - 30 ° = 60 °
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có A B x ^ = D B x ^ + D B A ^ = 90 ° + 30 ° = 120 °
Gọi các góc của tam giác đó lần lượt là A, B, C ( A, B, C \(\ne\)0 )
vì các góc của tam giác lần lượt tỉ lệ với 1, 2, 3 nên theo đề bài ta có :
\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}\) và \(A+B+C=180^o\)( định lí tổng 3 góc trong một tam giác )
Áp dụng tính chất dãy tỉ số bằng nhauta được :
\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{A+B+C}{1+2+3}=\frac{180^o}{6}\)\(=30\)
\(\Rightarrow\hept{\frac{A}{1}=30}\Rightarrow A=30.1=30^o\)
\(\Rightarrow\hept{\frac{B}{2}=30\Rightarrow}B=30.2=60^o\)
\(\Rightarrow\hept{\frac{C}{3}=30\Rightarrow}C=30.3=90^o\)
+ Xét ΔABCΔABC có Cˆ=900(cmt)C^=900(cmt)
=> ΔABCΔABC vuông tại C(đpcm).C(đpcm).
Vậy ΔABCΔABC vuông tại C.