N
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
K
cho tam giác abc góc a = 60 . phân giác bd và ce cắt nhau tại o . cm tam giác ode cân , BE + CD = BC
0
12 tháng 3 2023
Có `Delta ABC` cân tại `A=>AB=AC;hat(ABC)=hat(ACB)`
Có `hat(ABC)=hat(ACB)(cmt)`
mà `BD` là p/g `hat(ABC)`
`CE` là p/g `hat(ACB)`
nên `hat(B_1)=hat(C_1)`
Xét `Delta ABD` và `Delta ACE` có :
`{:(hat(B_1)=hat(C_1)(cmt)),(AB=AC(cmt)),(hat(A)-chung):}}`
`=>Delta ABD=Delta ACE(g.c.g)`
`=>BD=CE` ( 2 cạnh t/ứng )(đpcm)
13 tháng 3 2023
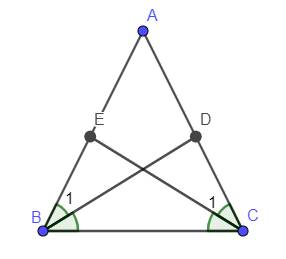
A B C D E
BD là đường phân giác của góc B nên ta có :
\(\widehat{ABD}=\widehat{CBD}=\dfrac{1}{2}\widehat{B}\) ( 1 )
CE là đường phân giác của góc C nên ta có :
\(\widehat{ACE}=\widehat{BCE}=\dfrac{1}{2}\widehat{C}\) ( 2 )
Từ ( 1 ) , ( 2 ) = > \(\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ADB và tam giác AEC ta có :
Góc A chung
AB = AC ( gt )
\(\widehat{ABD}=\widehat{ACE}\) ( cmt )
= > \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)
= > BD = CE ( 2 cạnh tương ứng )