Question

[hieu]

cho tam giác abc có hai đường trung tuyến bm và cn nếu bm=cn thì tam giác abc là tam giác gì

Answer 1

[HT.Phong (9A5)]

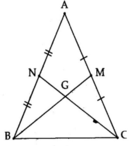
Do \(BM\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AM=CM\)

Và \(CN\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AN=BN\)

Mà \(BM=CN\left(gt\right)\)

Từ đó suy ra: \(AM=CM=AN=BN\)

Ta lại có: \(AM+CM=AC\)

Và \(AN+BN=AB\)

Nên: \(AM=CM=AN=BN\)

\(\Rightarrow AM+CM=AN+BN\)

\(\Rightarrow AC=AB\)

Vậy \(\Delta ABC\) có \(AC=AB\) là tam giác cân tại \(A\)

Answer 2

[Buddy]

Bổ sung cái hình nhầy:>>