Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B A D C E H K
câu a ta có AB=BE, BD chung và góc ABD=BDE do BD là phân giác của ABC
do đó hai tam giác ABD và EBD bằng nhau theo trường hợp cạnh góc cạnh,
b, do từ kết quả câu a ta có DEB=DA B=90 độ do đó DE vuông với EB , mà AH vuông góc với EB nên
DE //AH.
c. ta có \(KB=KA+AB=EC+EB=BC\)
mà AB=BE và góc B chung
do đó hai tam giác ABC và EBK bằng nhau theo trường hợp cạnh góc cạnh.
. dễ thấy AM và AB là tia phân giác của hai góc kề bù
do đó chúng vuông góc với nhau
nên tam giác DBM vuông tại D do đó \(\widehat{ABD}+\widehat{AMD}=90^0\)

a) xét 2 tam giác vuông ABD và EBD có:
ABD=EBD(gt)
BD(chung)
suy ra tam giác ABD = EBD(CH-GN)
suy ra DA=DE(đfcm)
b) góc B= góc A- góc C=90-30=60(1)
theo câu a, ta có;tam giác ABD = EBD(CH-GN) suy ra BA=BE(2)
từ (1)(2) suy ra tam giác BAE đều(đfcm)
c)theo câu b, ta có: tam giác ABE đều suy ra AB=BE=AE(3)
góc : DBE=60/2=30 và C=30 suy ra góc DBE=C
ta có: BDE=90-30=60
CDE=90-30=60
suy ra BDE=CDE
xét tam giác BDE và CDE có:
BDE=CDE(cmt)
BED=CED=90(gt)
DE(chung)
suy ra tam giác BDE =CDE(g.c.g)
suy ra EB=EC=1/2BC(4)
từ (3) (4) suy ra AB=BE=EC mà CE=1/2 BC suy ra AB=1/2BC(đfcm)

Thằng kia ko tl thì cút,đừng có làm phiền người khác.Đã bị 20 vé báo cáo rồi đấy

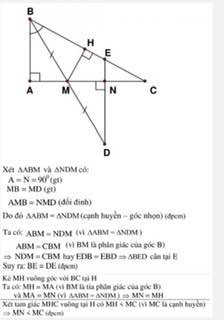
A B C M N H E D I I
Xét \(\Delta ABM\)và \(\Delta NDM\)có: \(\hept{\begin{cases}\widehat{A}=\widehat{DNM}=90^o\left(gt\right)\\MB=MD\left(gt\right)\\\widehat{AMB}=\widehat{NMD}\end{cases}}\Rightarrow\Delta ABM=\Delta NDM\left(ch-gn\right)\left(đpcm\right)\)
Ta có \(\widehat{ABM}=\widehat{NDM}\left(\Delta ABM=\Delta NDM\right)\)
\(\widehat{ABM}=\widehat{CBM}\)(BM là phân giác \(\widehat{B}\))
\(\Rightarrow\widehat{NDM}=\widehat{CBM}\)hay \(\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta BED\)cân tại E
=> BE=DE (đpcm)
Kẻ MH vuông góc với BC tại H
Ta có MH=MA (vì BM là tia phân giác của \(\widehat{B}\))
và MA=MN (\(\Delta ABM=\Delta NDM\))
=> MN=MH
Xét \(\Delta MHC\)vuông tại H có MH<MC (vì MC là cạnh huyền)
=> MN<MC (đpcm)

A B C D E F
a) Ez bạn tự làm nha, mình làm sơ sơ cũng 3-4 cách rồi.:)
b) Tam giác ABC cân tại A có đường p/g góc A xuất phát từ đỉnh đồng thời là đường trung trực nên \(AD\perp BC\). và BD = CD = BC/2
Xét tam giác ABD vuông tại D (chứng minh trên), theo định lí Pythagoras:
\(AB^2=BD^2+DA^2\Leftrightarrow10^2=\frac{BC^2}{4}+DA^2\)
\(=36+DA^2\Rightarrow AD=8\) (cm) (khúc này có tính nhầm gì thì tự sửa lại nha!)
Theo đề bài ta có AB = AC = 10 < BC = 12
Hay AC < BC. Theo quan hệ giữa góc và cạnh đối diện trong tam giác ABC ta có \(\widehat{ABC}< \widehat{BAC}\) (Cái khúc này không chắc, sai thì thôi)
c) Hướng dẫn:
\(\Delta\)EDB = \(\Delta\)FDC (cạnh huyền - góc nhọn)
Suy ra EB = FC. Từ đó suy ra AE = AF.
Suy ra tam giác AEF cân tại A suy ra \(\widehat{AEF}=\frac{180^o-\widehat{A}}{2}\) (1)
Mặt khác tam giác ABC cân tại A nên \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) suy ra đpcm

hinh tu ve :
Xet tamgiac AFN va tamgiac AEN co :
FE | AM (gt) => goc FNA = goc ANE = 90 do (dn) (1)
AN la tia phan giac cua goc CAB (gt) => goc FAN = goc NAE (dn) (2)
AN chung (3)
(1)(2)(3) => tamgiac AFN = tamgiac AEN (cgv - gnk)
=> AE = AF (dn)
b, ke BO = BE (O thuoc FE)

Tham khảo
Câu hỏi của Hot girl 2k5 - Toán lớp 7 - Học toán với OnlineMath
mik ko hieu cau c cho lam, ai giang giup mik cau c voi :((
A B C D E
Xét \(\Delta BAD\)và \(\Delta BED\):
BAD^ = BED^ = 90o
BD chung
ABD^ = EBD^
\(\Rightarrow\Delta BAD=\Delta BED\)(cạnh huyền _ góc nhọn)
\(\Rightarrow BA=BE\)(2 cạnh tương ứng)