N
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
1
CM
29 tháng 8 2018
+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
HA
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2022
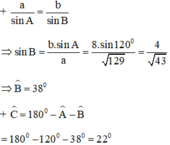
Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=7\)
Diện tích:
\(S_{ABC}=\dfrac{1}{2}ac.sinB=10\sqrt{3}\)
HA
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2022
\(C=180^0-\left(A+B\right)=77^04'\)
Áp dụng định lý hàm sin:
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\Rightarrow AC=\dfrac{AB.sinB}{sinC}=\dfrac{117.sin34^044'}{sin77^04'}\approx68,4\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)
b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)
c)
+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)
+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)
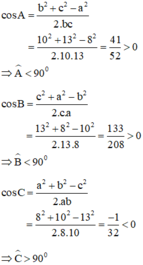
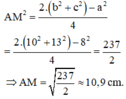
Góc A = 180 độ - (góc B + góc C) = 180 độ - (44 độ 30 phút + 64 độ) = 71 độ 30 phút.
Từ B kẻ BH vuông góc với AC tại H. Trong tam giác vuông BHC, ta có:
CosC = CH/BC => CH = BC*CosC = 17,4*Cos64độ = 17,4*0,4384 = 7,6277
SinC = BH/BC => BH = BC*SinC = 17,4*Sin64độ = 17,4*0,8988 = 15,6390
Trong tam giác vuông AHB, ta có:
SinA = BH/AB => AB = BH/SinA = 15,6390/Sin71độ30phút = 15,6390/0,9483 = 16, 4916 = c
CosA = AH/AB => AH = AB*CosA = c*Cos71độ30phút = 16,4916*0,3173 = 5,2329
AC = AH + CH = 5,2329 + 7,6277 = 12,8606 = b
Vậy: A = 71độ30phút, b = 12,8606, c= 16,4916
\(\widehat{A}=180^O-\left(44^O33'+64^O\right)=71^O27'\)
THEO ĐỊNH LÝ SIN,TA CÓ:
\(\frac{a}{\sin A}=2R\Rightarrow R=\frac{a}{2.\sin A}=\frac{17,4}{2.\sin71^O27'}\approx9,2\)
\(\frac{b}{\sin B}=2R\Rightarrow b=2R.\sin B=2.9,2.\sin44^O30'\approx12,9\)
\(\frac{c}{\sin C}=2R\Rightarrow c=2R.\sin C=2.9,2.\sin64^O\approx16,5\)