

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



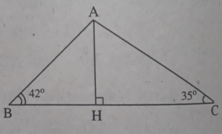
Đặt AH = h thì rõ ràng BH = h.cotg (ABH) = h. cotg 42 °
CH = h.cotg (ACH) = h.cotg 35 ° (để ý rằng H thuộc đoạn BC vì 35 ° , 42 ° đều là góc nhọn).
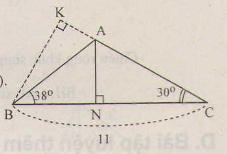
Do đó: 7 = BC = BH + CH = h(cotg 42 ° + cotg 35 ° ), suy ra
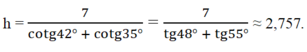

Xét ΔANB vuông tại N có
\(AN=AB\cdot\sin B\)
nên \(AN\simeq6,772\left(cm\right)\)
XétΔACN vuông tại N có
\(AC=\dfrac{AN}{\sin C}=13,544\left(cm\right)\)

a) Trong tam giác vuông BCH, ta có:
CH=BC.sinB^=12.sin60≈10,392 (cm)
Trong tam giác vuông ABC, ta có:
\(A\)=180−(60+40)=80
Trong tam giác vuông ACH, ta có:
\(AC=\dfrac{CH}{sinA}=\dfrac{10,932}{sin80}=10,552\left(cm\right)\)
b) Kẻ AK⊥BCAK⊥BC
Trong tam giác vuông ACK, ta có:
AK=AC.sinC≈10,552.sin40=6,783 (cm)
Vậy SABC=12.AK.BC≈12.6,783.12=40,696 (cm2)

a: AB=BC*cos60=6*1/2=3cm
AC=căn 6^2-3^2=3*căn 3\(\simeq5.2\left(cm\right)\)
b: HB=AB^2/BC=1,5cm
HC=6-1,5=4,5cm
c) Tam giác BCD, có: BC=BD=> Tam giác BCD cân tại B=>BDC=BCD
Mặt khác: BDC+BCD=ABC=60 độ (tính chất góc ngoài của tam giác)
=>BDC=BCD=30 độ
Tam giác ABC vuông tại A, có: ABC+ACB=90 độ
=>ACB=90 độ-ABC=90 độ-60 độ=30 độ
=>ACD= DCB+BCA=30 độ+30 độ= 60 độ
Xét 2 tam giác ABC và ACD,có:
ABC=ACD=60 độ
ACB=ADC=30 độ
=> tam giác ABC đồng dạng tam giác ACD (g-g)
=>\(\dfrac{AB}{BC}=\dfrac{AC}{CD}\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}\) (vì BD=BC)

Xét ΔABC vuông tại A có
\(AB=BC\cdot\cos30^0=4\sqrt{3}\simeq6,928\left(cm\right)\)

a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

a) Kẻ BK⊥ACBK⊥AC
Ta được: ˆKBC=60∘KBC^=60∘ và ˆKBA=60∘=60∘−38∘=22∘KBA^=60∘=60∘−38∘=22∘
Xét tam giác KBC vuông tại K có:
BK=BC⋅sinC=11⋅sin30∘=5,5(cm)BK=BC⋅sinC=11⋅sin30∘=5,5(cm)
Xét tam giác KBA vuông tại K có:
AB=BKcos22∘=5,5cos22∘≈5,932(cm).AB=BKcos22∘=5,5cos22∘≈5,932(cm).
Xét tam giác ABN vuông tại N có:
AN=AB⋅sin38∘≈5,932⋅sin38∘≈3,652(cm)AN=AB⋅sin38∘≈5,932⋅sin38∘≈3,652(cm)
b) Xét tam giác ANC vuông tại N có AC=ANsinC≈

Kẻ BH vuông góc với AC
Xét ΔABH vuông tại H có \(BH=AB\cdot\sin A\simeq1,7101\left(cm\right)\)
\(S_{ABC}=\dfrac{BH\cdot AC}{2}=6.8404\left(cm^2\right)\)