Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ A kẻ đường cao AH vuông góc với BC , từ B kẻ đường cao BK vuông góc với AC
=> AH = sinC x AC = sin 500 x 35 = a
Ta có : AB = \(\frac{AH}{sinB}=\frac{a}{sinB}=b\)
BK = \(sinA\times AB=sin\left(180^o-60^o-50^o\right)=sin70^o\times b\)= c
=> S . ABC = 1/2AC x BK = 1/2 x 35 x c =..........
a,b,c mình đặt thay cho độ dài AH , AB, BK
Sao bạn không tính hẳn AH, AB, BK mà phải kí hiệu a, b,c vậy?

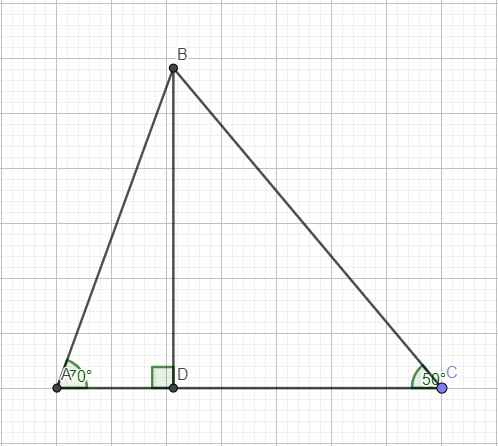
Kẻ AH vuông góc với BC
Trong tam giác vuông AHC ta có:
\(cosC=\frac{HC}{AC}\Rightarrow HC=cosC.AC=cos50.35\approx22cm\)
\(\Rightarrow AH=\sqrt{AC^2-HC^2}=\sqrt{35^2-22^2}=\sqrt{741}cm\)
Trong tam giác vuông AHB ta có:
\(sinB=\frac{AH}{AB}\Rightarrow AB=\frac{AH}{sinB}=\frac{\sqrt{741}}{sin60}=2\sqrt{247}cm\)
\(\Rightarrow HB=\sqrt{AB^2-AH^2}=\sqrt{\left(2\sqrt{247}\right)^2-741}=\sqrt{247}cm\)
Vậy \(S_{ABC}=\frac{AH\left(HB+HC\right)}{2}=\frac{\sqrt{741}.\left(\sqrt{247}+22\right)}{2}\approx513cm\)

Kẻ AH vuông góc với BC
Trong tam giác vuông AHC ta có:
cosC=HC/AC⇒HC=cosC.AC=cos50.35≈22cm
⇒AH=√AC^2−HC^2=√35^2−22^2=√741cm
Trong tam giác vuông AHB ta có:
sinB=AH/AB⇒AB=AH/sinB=√741/sin60=2√247cm
⇒HB=√AB^2−AH^2=√(2√247)^2−741=√247cm
Vậy SABC=AH(HB+HC)/2=√741.(√247+22)/2≈513\(cm^2\)

1.
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)

trong tam giac AHC co \(AH=AC\cdot\sin C=35\cdot\sin50\approx26,8\)
ap dung dl pitago vao AHC ta tinh dc \(HC=AC^2-AH^2\approx22,5\)
tg tu trong tam giac ABH co \(BH=\cot60\cdot26,8\approx15,5\)
\(\Rightarrow BC=BH+CH=38\)
\(\Rightarrow SABC=\frac{1}{2}BC\cdot AH=509,2\)

Ta có \(CH=AC.cos\widehat{C}=35.cos50^o\)
\(AH=AC.sin\widehat{C}=35.sin50^o\)
\(BH=AH.cot\widehat{B}=35.sin50^o.cot60^o\)
\(\Rightarrow BC=BH+CH=35.cos50^o+35.sin50^o.cot60^o\)
\(\Rightarrow S_{ABC}=\frac{AH.BC}{2}=\frac{35.sin50^o\left(35.cos50^o+35.sin50^o.cot60^o\right)}{2}\)

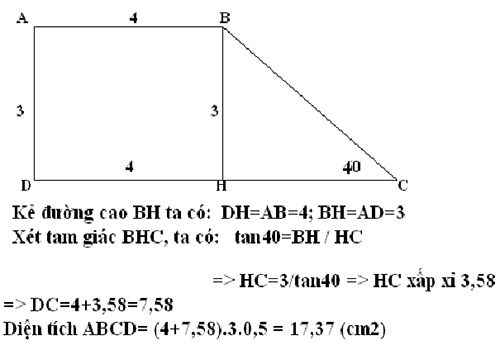
a. Ta có: AB2 + AC2 = 212 + 282 = 1225
BC2 = 352 = 1225
=> BC2 = AB2 + AC2
=> Tam giác ABC là tam giác vuông (Định lý Pytago đảo)
Diện tích tam giác ABC
\(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.21.28=294\left(cm^2\right)\)
b. \(sinB=\frac{AC}{BC}=\frac{28}{35}=\frac{4}{5}\)
\(sinC=\frac{AB}{BC}=\frac{21}{35}=\frac{3}{5}\)
c. Ta có: \(\frac{BD}{DC}=\frac{AB}{AC}=\frac{21}{28}=\frac{3}{4}\)\(\)
=> 4BD = 3DC
<=> 4BD = 3(BC - BD)
<=> 7BD = 3BC
<=> 7BD = 3 . 35
=> BD = 15 (cm)
=> DC = 20 (cm)

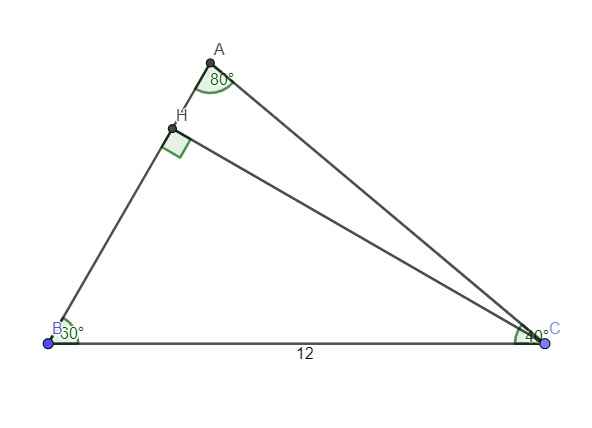
Ta có: \(A=180^0-\left(B+C\right)=80^0\)
Trong tam giác vuông BCH:
\(sinB=\dfrac{CH}{BC}\Rightarrow CH=BC.sinB=12.sin60^0=6\sqrt{3}\left(cm\right)\)
\(cotB=\dfrac{BH}{CH}\Rightarrow BH=CH.cotB\) (1)
Trong tam giác vuông ACH:
\(sinA=\dfrac{CH}{AB}\Rightarrow AB=\dfrac{CH}{sinA}=\dfrac{6\sqrt{3}}{sin80^0}\approx10,6\left(cm\right)\)
\(cotA=\dfrac{AH}{CH}\Rightarrow AH=CH.cotA\) (2)
(1);(2) \(\Rightarrow AH+BH=CH\left(cotA+cotB\right)\)
\(\Rightarrow AB=CH\left(cotA+cotB\right)\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}CH.AB=\dfrac{1}{2}.CH^2\left(cotA+cotB\right)=\dfrac{1}{2}.\left(6\sqrt{3}\right)^2\left(cot80^0+cot60^0\right)\approx40,7\left(cm^2\right)\)