Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+60^0=90^0\)
=>\(\widehat{ABC}=30^0\)
Xét ΔCAD có CA=CD
nên ΔCAD cân tại C
b: Xét ΔCAM và ΔCDM có
CA=CD
AM=DM
CM chung
Do đó: ΔCAM=ΔCDM
c: Ta có: ΔCAM=ΔCDM
=>\(\widehat{ACM}=\widehat{DCM}\)
=>\(\widehat{ACP}=\widehat{DCP}\)
Xét ΔPAC và ΔPDC có
CA=CD
\(\widehat{PCA}=\widehat{PCD}\)
CP chung
Do đó: ΔPAC=ΔPDC
=>\(\widehat{PAC}=\widehat{PDC}\)
mà \(\widehat{PAC}=90^0\)
nên \(\widehat{PDC}=90^0\)
=>PD\(\perp\)BC

a) Xét ΔABC có
BC>AB(15cm>7cm)
mà góc đối diện với cạnh BC là \(\widehat{BAC}\)
và góc đối diện với cạnh AB là \(\widehat{ACB}\)
nên \(\widehat{BAC}>\widehat{ACB}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)

a: Xét ΔABC có AB<BC
nên \(\widehat{ACB}< \widehat{BAC}\)
b: Xét ΔAMB có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔAMB cân tại A
mà \(\widehat{B}=60^0\)
nên ΔAMB đều

a)Xét tam giác ABC có:
góc ABC + góc BAC + góc ACB =180 độ. Thay số:
60 độ + 90 độ + góc ACB = 180 độ
góc ACB =180 độ - (60 độ + 90 độ)
góc ACB = 30 độ
b)Xét tam giác AMN và tam giác CMN có:
AM = CM (M là trung điểm của AC)
MN chung
góc AMN = góc CMN =90 độ(MN vuông góc với AC)
Suy ra :tam giác AMN = tam giác CMN(c.g.c)
CÒN LẠI MÌNH CHƯA NGHĨ RA. MONG BẠN THÔNG CẢM![]()

a, xét tam giác ABM và tam giác KBM có: AB=BK, BM chung, góc ABM= góc KBM
suy ra 2 tam giác trên bằng nhau
hok tốt
tu ve hinh :
xet tamgiac ABM va tamgiac KBM co : MB chung
goc ABM = goc MBK do BM la phan giac cua goc ABC (gt)
AB = AK (gt)
=> tammgiac ABM = tamgiac KBM (c - g - c)
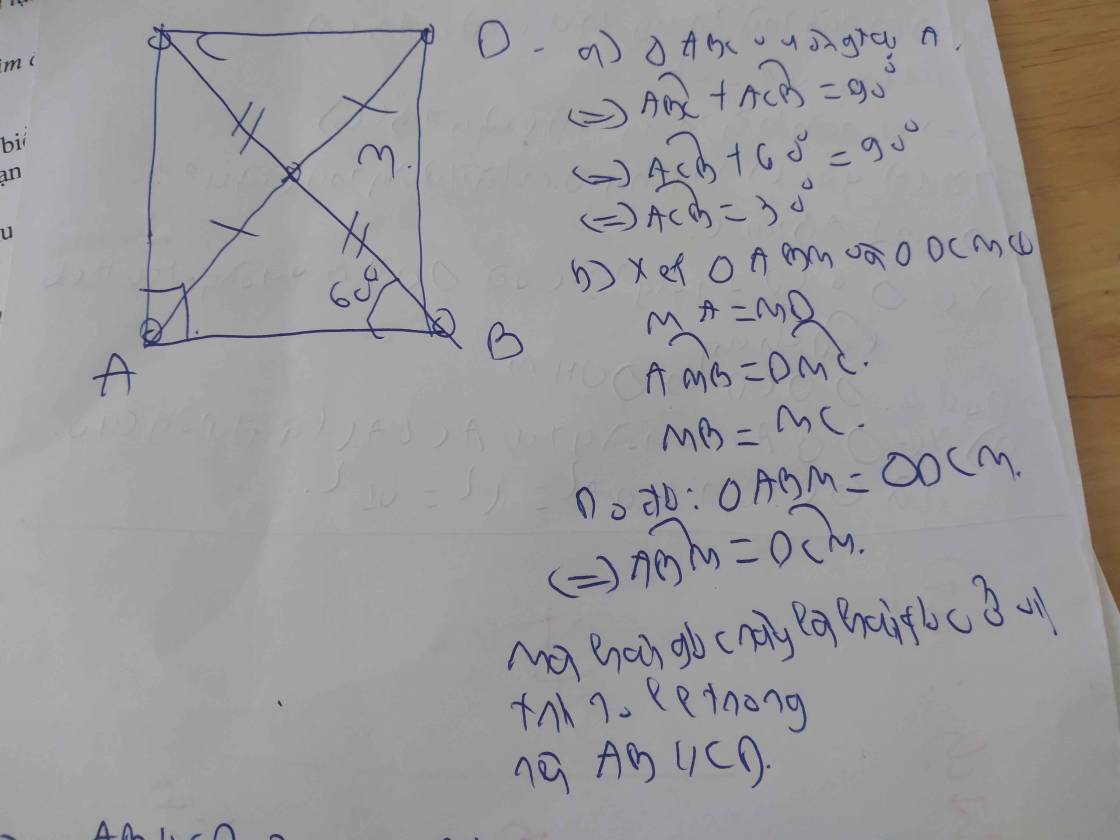

Ta có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\Rightarrow\widehat{BAC}=180^0-60^0-30^0=90^0\)
Do đó tam giác ABC vuông tại A
Trên tia đối MA lấy D sao cho M là trung điểm AD
\(\left\{{}\begin{matrix}CM=MB\\AM=MD\\\widehat{CMA}=\widehat{BMD}\left(đối.đỉnh\right)\end{matrix}\right.\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\\ \Rightarrow AC=BD;\widehat{CAM}=\widehat{MDB}\)
Mà \(\widehat{CAM}+\widehat{MAB}=\widehat{BAC}=90^0\Rightarrow\widehat{MDB}+\widehat{MAB}=90^0\)
Mà \(\widehat{MDB}+\widehat{MAB}+\widehat{DBA}=180^0\Rightarrow\widehat{DBA}=90^0\)
\(\left\{{}\begin{matrix}\widehat{DBA}=\widehat{BAC}\left(=90^0\right)\\AC=BD\\AB.chung\end{matrix}\right.\Rightarrow\Delta BAC=\Delta ABD\left(c.g.c\right)\\ \Rightarrow AD=BC\\ \Rightarrow AM=MB\left(\dfrac{1}{2}AD=\dfrac{1}{2}BC\right)\)
Do đó tam giác ABM cân tại M
Mà có \(\widehat{ABM}=60^0\) nên tam giác ABM đều
Vì tam giác ABM đều nên \(AB=BM=\dfrac{1}{2}BC\)