Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAMD và ΔAMC có
AM chung
MD=MC
AD=AC
Do đó: ΔAMD=ΔAMC
b: Xét ΔNDC có
NM là đường cao
NM là đường trung tuyến
Do đó:ΔNDC cân tại N
hay ND=NC

abc= 30 độ vì tổng 3 góc của 1 tam giác
=> AC>AB
=> bước sau tự lm

a, vì CA=CE(GT) =>TAM GIÁC ACE CÂN TẠI C=> GÓC CAE= GÓC AEC
b,vì AB<AC=>góc ABC>góc ACB(quan hệ giữa góc và cạnh trong 1 tam giác)
c, vì AH là đường cao => AH là đường vuông góc
TA CÓ AB=BD, AC=CE MÀ AB<AC=>BD<CE=>HD<HE(quan hệ giữa đx và hc)

a). Ta có AM là đường trung trực của đoạn thẳng BC => AM\(\perp\) BC và BM=CM
Xét tam giác AMB vuông tại M và tam giác AMC vuông tại M có:
AM là cạnh chung.
BM=CM (cmt)
=> Tam giác AMB=tam giác AMC (hai cạnh góc vuông)
b). Tam giác AMB=tam giác AMC
=> AB=AC (hai cạnh tương ứng)
=> \(\widehat{BAM}\) = \(\widehat{CAM}\) (hai góc tương ứng)
=> \(\widehat{ABM}=\widehat{ACM}\) (hai góc tương ứng)
c). Xét tam giác ANB và tam giác ANC có:
AB=AC (cmt)
\(\widehat{BAN}=\widehat{CAN}\) (\(\widehat{BAM}=\widehat{CAM};N\in\) AM)
AN là cạnh chung.
=> Tam giác ANB=tam giác ANC (c.g.c)
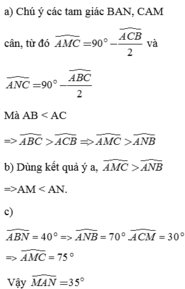
a) Vì AB<AC(gt)
mà AM=AC(gt)
và A,B,M thẳng hàng(gt)
nên điềm B nằm giữa hai điểm A và M
hay tia CB nằm giữa hai tia CA và CM
\(\Leftrightarrow\widehat{ACB}+\widehat{MCB}=\widehat{ACM}\)
hay \(\widehat{ACM}>\widehat{ACB}\)