Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

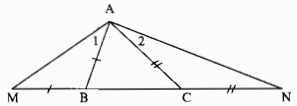
Trong ∆ABC có AB < AC
⇒ góc ABC= góc ACB (đối diện cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt)
⇒ góc ∆ABM cân tại B
⇒ góc M = góc A1(tính chất tam giác cân)
Trong ∆ABM ta có có góc ngoài tại đỉnh B
góc ABC= góc M+ góc A1
Suy ra: góc M=12 góc ABC (2)
Ta có: AC = CN (gt)
⇒ ∆CAN cân tại C⇒ góc N= góc A2 (tính chất tam giác cân)
Trong ∆CAN ta có góc ACB là góc ngoài tại đỉnh C.
⇒góc ACB= góc N+ góc A2
Suy ra: góc N=12 góc ACB (3)
Từ (1), (2) và (3) suy ra: góc M > góc N
b) Trong ∆AMN ta có: góc M> góc N

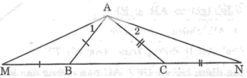
Trong ΔABC, ta có AC > AB
Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt) ⇒ ΔABM cân tại B
Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)
Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B
Suy ra: ∠(ABC) = ∠(AMB) + ∠A1 hay : ∠(ABC) = 2.∠(AMB)
Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)
Lại có: AC = CN (gt) ⇒ ΔACN cân tại C
Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)
Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C
Suy ra: ∠(ACB) = ∠(ANC) + ∠A2 hay ∠(ACB) = 2∠(ANC)
Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)
Từ (1), (2) và (3) suy ra: ∠(AMB) > ∠(ANC) .

Ta có bài toán sau: Xét tam giác ABC vuông tại A, tam giác MNP vuông tại M.
Nếu \(BC=NP\) hoặc \(BC\equiv NP\)thì \(AC>MP\Leftrightarrow\widehat{ABC}>\widehat{MNP}.\)
Chứng minh:
A B C M N P D O
Trên mặt phẳng chứa hai tam giác, lấy điểm D sao cho \(\Delta BDC=\Delta NMP\) (D,A khác phía so với BC)
Ta có \(\widehat{MNP}=\widehat{DBC},MP=DC\)
Xét tam giác ACD: \(AC>MP=CD\), suy ra \(\widehat{ADC}>\widehat{DAC}\)(1)
Gọi O là trung điểm BC, dễ thấy O cách đều A,B,C,D. Do đó:
\(\widehat{ADC}=\frac{1}{2}\widehat{AOC}=\widehat{ABC};\widehat{DAC}=\frac{1}{2}\widehat{DOC}=\widehat{DBC}=\widehat{MNP}\)(2)
Từ (1),(2) suy ra \(\widehat{ABC}>\widehat{MNP}\). Tương tự ta có thể chứng minh chiều ngược lại của bài toán.
Giải:
A B C M N D H K
Xét \(\Delta BMC\) và \(\Delta CNB\): Chung cạnh BC, BM = CN, \(\widehat{MBC}< \widehat{NCB}\); suy ra \(CM< BN\)
Dựng hình bình hành BMDN, ta có \(CM< BN=MD\)
Xét tam giác CMD: \(CM< MD\), suy ra \(\widehat{MDC}< \widehat{MCD}\)
Dễ thấy tam giác CND cân tại N, do vậy \(\widehat{MDC}-\widehat{NDC}< \widehat{MCD}-\widehat{NCD}\)
Hay \(\widehat{NDM}< \widehat{NCM}\). Gọi H và K là hình chiếu của N trên MD và MC.
Theo bài toán trên thì \(NH< NK\), từ đó \(\widehat{NMH}< \widehat{NMK}\)hay \(\widehat{BNM}< \widehat{CMN}\)(đpcm).

Câu hỏi của Nguyễn Tiến Vững - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!
Tên gì mà độc thế ? Đảo ngược tên lại đi là Mỹ Lệ
đảo lại trùng tên òy híhí