Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác ABC có AB = AC
=> Tam giác ABC là tam giác cân
Ta có : AM là đường trung tuyến
=> AM cũng là đường vuông góc
( Ta được tam giác vuông ABM và ACM
Xét tam giác vuông ABM
Theo định lí pi-ta-go, ta có :
\(AM^2+MB^2=AB^2\)
hay \(8^2+MB^2=10^2\)
\(\Rightarrow MB^2=AB^2-AM^2=10^2-8^2=100-64=36\)
\(\Rightarrow MB=\sqrt{36}=6\left(cm\right)\)
Ta có : \(MB=\dfrac{1}{2}BC\left(M\cdot là\cdot trung\cdotđiểm\cdot của\cdot BC\right)\)
\(\Rightarrow BC=12cm\)
Xét tam giác ABC: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AM là đường trung tuyến (M là trung điểm của BC).
=> AM là đường cao (Tính chất các đường trong tam giác cân).
=> AM vuông góc BC.
Xét tam giác AMB vuông tại M:
\(AB^2=AM^2+BM^2\left(Pytago\right).\\ \Rightarrow10^2=8^2+BM^2.\\ \Rightarrow BM^2=36.\Rightarrow BM=6\left(cm\right).\)
Mà \(2BM=BC\) (M là trung điểm của BC).
=> BC = 12 (cm).

a: Xét ΔABC có
AM là trung tuyến
AM=BC/2
=>ΔABC vuông tại A
b: AB=căn 10^2-8^2=6cm
c: GM=1/3*AM=5/3(cm)

a) Xét tam giác ABC có:
BC2 = 102 = 100 (cm)
AB2 + AC2 = 62 + 82 = 36 + 64 = 100 (cm)
=> BC2 = AB2 + AC2 (= 100)
=> Tam giác ABC vuông tại A (định lý Pytago đảo)
b) MB = MD (gt) => M là trung điểm BD
Xét Tứ giác ABCD có:
M là trung điểm của BD (cmt)
M là trung điểm của AC (gt)
=> ABCD là hình bình hành (dhnb)
=> AB // CD (Tính chất hình bình hành)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC và AB=EC
c: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔBCD cân tại C
d: Xét ΔOBC có
OM là đường cao
OM là đường trung tuyến
Do đó: ΔOBC cân tại O
Suy ra: OB=OC(1)
Xét ΔOBD có
OA là đường cao
OA là đường trung tuyến
Do đó: ΔOBD cân tại O
Suy ra: OB=OD(2)
Từ (1) và (2) suy ra OB=OC=OD
hay O cách đều ba đỉnh của ΔBDC

a)
Sửa đề: ΔBIM=ΔCKM
Xét ΔBIM vuông tại I và ΔCKM vuông tại K có
BM=CM(M là trung điểm của BC)
\(\widehat{IBM}=\widehat{KCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBIM=ΔCKM(cạnh huyền-góc nhọn)

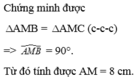

Xét ΔABM vuông tại M có
\(AB^2=BM^2+AM^2\)
=>BM=6(cm)
=>BC=12(cm)
Vì tam giác ABC cân nên AM là đường trung tuyến đồng thời là đường cao Theo định lí Pytago cho tam giác AMB vuông tại M
BM = \(\sqrt{AB^2-AM^2}=6\)cm
=> BC = 2BM = 12 cm