Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí côsin trong tam giác ta có:
B C 2 = 2 2 + 5 2 − 2.2.5. cos 45 ° = 29 − 10 2 ⇒ B C = 29 − 10 2
Chọn B


a) Đặt độ dài cạnh AB là x (\(x > 0\))
Theo giả thiết ta có độ dài \(AC = AB + 2 = x + 2\)
Áp dụng định lý pitago trong tam giác vuông ta có
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{x^2} + {{\left( {x + 2} \right)}^2}} = \sqrt {2{x^2} + 4x + 4} \)
b) Chu vi của tam giác là \(C = AB + AC + BC\)
\( \Rightarrow C = x + \left( {x + 2} \right) + \sqrt {2{x^2} + 4x + 4} = 2x + 2 + \sqrt {2{x^2} + 4x + 4} \)
Theo giả thiết ta có
\(\begin{array}{l}C = 24 \Leftrightarrow 2x + 2 + \sqrt {2{x^2} + 4x + 4} = 24\\ \Leftrightarrow \sqrt {2{x^2} + 4x + 4} = 22 - 2x\\ \Rightarrow 2{x^2} + 4x + 4 = {\left( {22 - 2x} \right)^2}\\ \Rightarrow 2{x^2} + 4x + 4 = 4{x^2} - 88x + 484\\ \Rightarrow 2{x^2} - 92x + 480 = 0\end{array}\)
\( \Rightarrow x = 6\) hoặc \(x = 40\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} + 4x + 4} = 22 - 2x\) ta thấy chỉ có \(x = 6\) thỏa mãn phương trình
Vậy độ dài ba cạnh của tam giác là \(AB = 6;AC = 8\) và \(BC = 10\)(cm)

c: \(AM^2=\dfrac{2\cdot\left(AB^2+AC^2\right)-BC^2}{4}=\dfrac{2\cdot\left(48^2+14^2\right)-50^2}{4}=625\)
nên AM=25(cm)
a: Xét ΔAHB vuông tại H có
\(AB^2=AH^2+HB^2\)
nên AH=16(cm)
Xét ΔAHC vuông tại H và ΔBKC vuông tại K có
\(\widehat{C}\) chung
Do đó: ΔAHC\(\sim\)ΔBKC
Suy ra: \(\dfrac{AH}{BK}=\dfrac{HC}{KC}=\dfrac{AC}{BC}\)
=>16/BK=20/24=5/6
=>BK=19,2(cm)

Dựng hình bình hành ABDC.
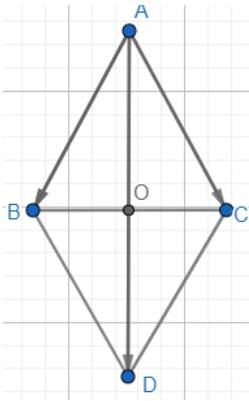
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)

a: vecto AB=(1;1)
vecto AC=(2;6)
vecto BC=(1;5)
b: \(AB=\sqrt{1^2+1^2}=\sqrt{2}\)
\(AC=\sqrt{2^2+6^2}=2\sqrt{10}\)
\(BC=\sqrt{1^2+5^2}=\sqrt{26}\)
=>\(C=\sqrt{2}+2\sqrt{10}+\sqrt{26}\)
c: Tọa độ trung điểm của AB là:
x=(1+2)/2=1,5 và y=(-1+0)/2=-0,5
Tọa độ trung điểm của AC là;
x=(1+3)/2=2 và y=(-1+5)/2=4/2=2
Tọa độ trung điểm của BC là:
x=(2+3)/2=2,5 và y=(0+5)/2=2,5
d: ABCD là hình bình hành
=>vecto AB=vecto DC
=>3-x=1 và 5-y=1
=>x=2 và y=4
