Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tự kẻ hình nha
a) vì AB=AC=> tam giác ABC cân A=> ABC=ACB=180-90/2=45 độ
xét tam giác ABM và tam giác ACM có
AB=AC(gt)
ABC=ACB(cmt)
BM=CM(gt)
=> tam giác ABM= tam giác ACM(cgc)
b) phải là AM//CK nha
từ tam giác ABM= tam giác ACM=> AMB=AMC(hai góc tương ứng)
mà AMB+AMC=180 độ (kề bù)
=> AMB=AMC=180/2=90 độ=> AM vuông góc với BC, CK vuông góc với BC
=> AM//CK
c) vì tam giác BCK vuông tại C=> CBK+BKC=90 độ=> BKC=90-45=45 độ

a, xét tam giác ABM và tam giác ACM có
AB=AC
BM=CM do M là trung điểm của BC
AM là cạnh chung
=> tam giác ABM =tam giác ACM c.c.c
=> góc B = góc C do là 2 góc tương ứng
vì tam giác ABM =tam giác ACM nên góc BMA= góc AMC (2 góc tương ứng
mà ^BMA + ^AMC =180 độ do là 2 góc kề bù
mà BMA = AMC nên BMA =AMC =180 độ :2 =90 độ
=> AM vuông góc với BC

Bài 2
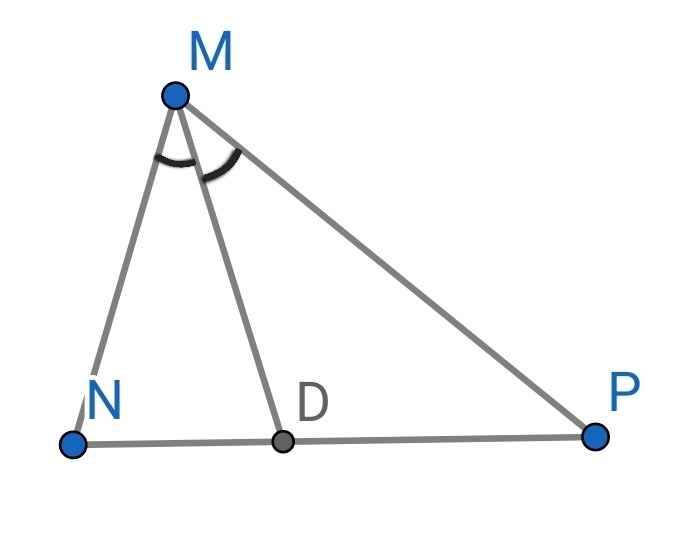
Ta có:
∠N + ∠DMN + ∠MDN = 180⁰ (tổng các góc trong ∆MDN)
⇒ ∠NMD = 180⁰ - (∠N + ∠MDN) (1)
∠P + ∠MDP + ∠PMD = 180⁰ (tổng các góc trong ∆MDP)
⇒ ∠PMD = 180⁰ - (∠MDP + ∠P) (2)
Do MD là tia phân giác của ∠NMP (gt)
⇒ ∠NMD = ∠PMD (3)
Từ (1), (2) và (3) ⇒ ∠DMP + ∠P = ∠N + ∠DMN
⇒ ∠DMP - ∠DMN = ∠N - ∠P
Bài 1
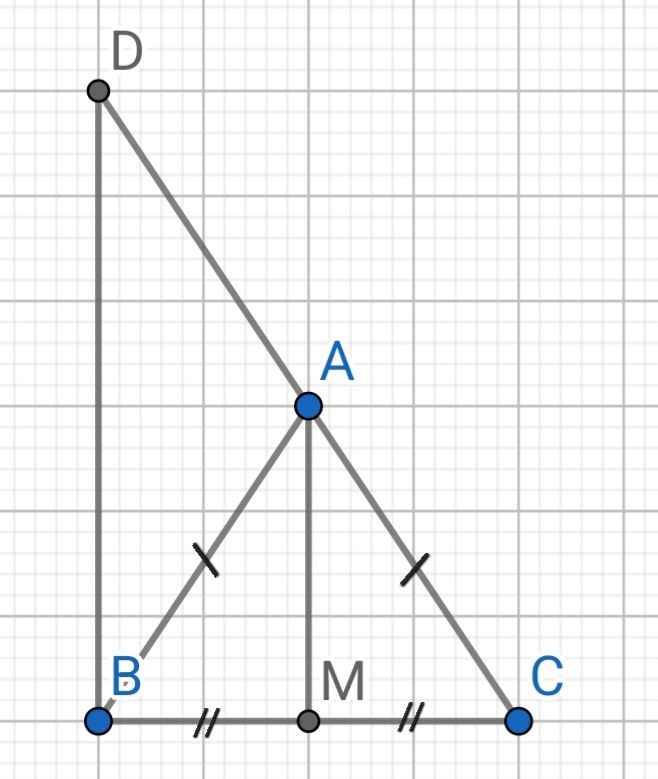 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆ABM và ∆ACM có:
AM là cạnh chung
AB = AC (gt)
MB = MC (cmt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
Mà BD ⊥ BC (gt)
⇒ BD // AM
c) Do ∆ABM = ∆ACM (cmt)
⇒ ∠BAM = ∠CAM (hai góc tương ứng)
Do BD // AM (cmt)
⇒ ∠ADB = ∠CAM (đồng vị)
∠ABD = ∠BAM (so le trong)
Mà ∠BAM = ∠CAM (cmt)
⇒ ∠ABD = ∠ADB

tự kẻ hình nha
a) vì tam giác ABC cân A=> AB=AC
xét tam giác ABM và tam giác ACM có
A1=A2(gt)
AB=AC(cmt)
AM chung
=> tam giác ABM= tam giác ACM(cgc)
=> AMB=AMC(hai góc tương ứng)
mà AMB+AMC=180 độ( kề bù)
=> AMB=AMC=180/2=90 độ=> AM vuông góc với BC
b) từ tam giác AMB= tam giác AMC=> BM=CM( hai cạnh tương ứng)
=> M là trung điểm BC=> AM là trung tuyến
BQ là trung tuyến
mà AM giao BQ tại G=> G là trọng tâm của tam giác ABC
c) ta có BC=BM+CM mà BM=CM=> BM=CM=BC/2=18/2=9 cm
ta có AM^2=AB^2-BM^2=15^2-9^2=225-81=144=12^2=> AM=12
vì G là trọng tâm của tam giác ABC=> AG=2/3AM=> AG=12*2/3=8 cm
d) vì MD//AC=> CAM=AMD( so le trong)
mà CAM=BAM(gt)
=> BAM=AMD=> tam giác AMD cân D=> AD=DM
vì tam giác ABM vuông tại M=> ABM+BAM=90 độ=> ABM=90 độ-BAM
vì AMD+DMB=AMB=> DMB=90 độ-AMD
mà AMD=BAM (cmt)
=> DMB=ABM=> tam giác DMB cân D=> BD=DM=> BD=AD=> D là trung điểm AB=> DC là trung tuyến
mà G là trọng tâm => G thuộc CD=> D, G, C thẳng hàng

