Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

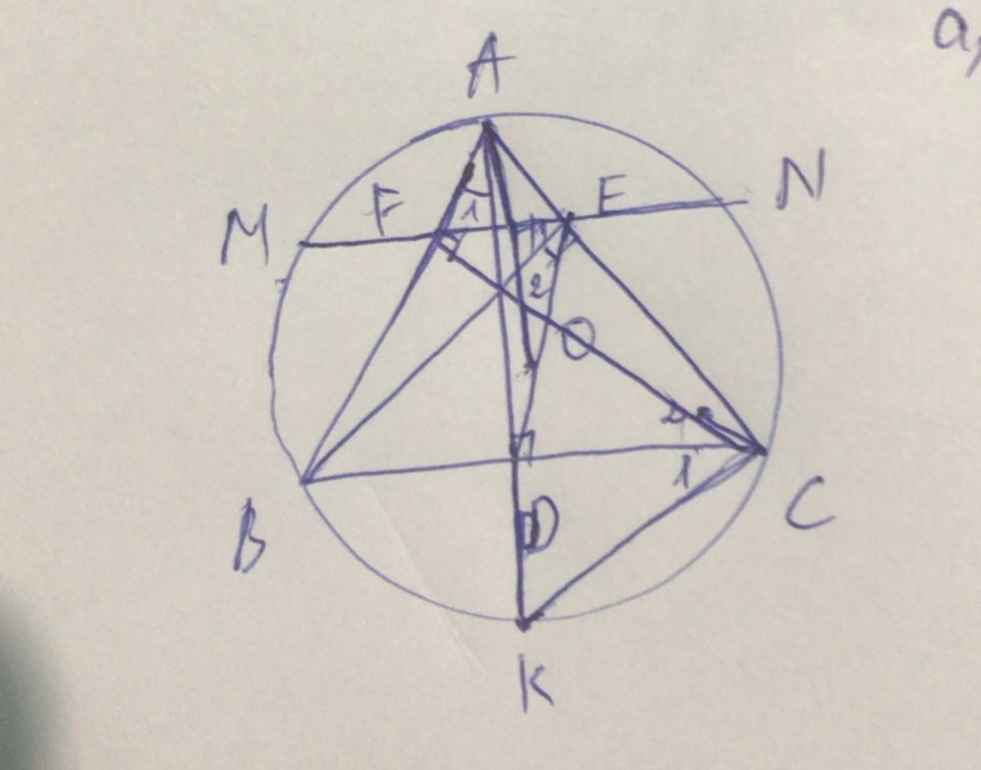
a) Ta có: \(\widehat{CFB}=90^0\)(CF⊥AB)
nên F nằm trên đường tròn đường kính CB(Định lí)(1)
Ta có: \(\widehat{CEB}=90^0\)(BE⊥AC)
nên E nằm trên đường tròn đường kính CB(Định lí)(2)
Từ (1) và (2) suy ra F,E cùng nằm trên đường tròn đường kính CB
hay B,E,F,C cùng thuộc một đường tròn(đpcm)
Tâm I của đường tròn ngoại tiếp tứ giác BEFC là trung điểm của CB
b) Ta có: BEFC là tứ giác nội tiếp(cmt)
nên \(\widehat{EFC}=\widehat{EBC}\)(Cùng nhìn cạnh EC)
\(\Leftrightarrow\widehat{KFC}=\widehat{KBE}\)
Xét ΔKFC và ΔKBE có
\(\widehat{FKB}\) chung
\(\widehat{KFC}=\widehat{KBE}\)(cmt)
Do đó: ΔKFC∼ΔKBE(g-g)
⇒\(\dfrac{KF}{KB}=\dfrac{KC}{KE}\)(Các cặp cạnh tương ứng tỉ lệ)
⇒\(KE\cdot KF=KB\cdot KC\)(đpcm)

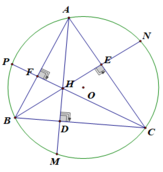
b) Xét tứ giác BFEC có:
∠(BFC) = 90 0 (Do CF là đường cao)
∠(BEC ) = 90 0 (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn

xét tứ giác BFHD có
góc BFH + góc BDH = 180
mà nó là 2 góc đối => nội tiếp => góc FDH = góc FBE
chứng minh tương tự với tứ giác CEHD
=> góc HDE = góc HCE
Xét tứ giác BFEC có
góc BFC = góc BEF = 90
mà nó là 2 góc kề => tứ giác nội tiếp
mà góc BEC = 1/2 sđ BC = 90 => SĐ BC = 180 => BC là đường kính mà I là trung điểm BC => I là tâm đường tròn ngoại tiếp tứ giác BFEC
=> góc FIE = góc FBE + góc FCE
=> Góc FIE = góc FDH+góc HDE => góc FIE = góc FDE
mà nó là 2 góc kề => nội tiếp
=> điều phải cm

a) Ta có: \(\widehat{BFC}=90^0\)(CF\(\perp\)AB)
nên F nằm trên đường tròn đường kính BC(Định lí)(1)
Ta có: \(\widehat{BEC}=90^0\)(BE\(\perp\)AC)
nên E nằm trên đường tròn đường kính BC(Định lí)(2)
Từ (1) và (2) suy ra F,E cùng nằm trên đường tròn đường kính BC
hay B,F,E,C cùng thuộc một đường tròn(đpcm)