Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
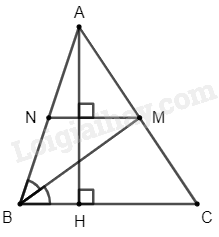
\(NM \bot AH\) (gt)
\(BC \bot AH\) (gt)
Suy ra \(NM\) // \(BC\)
Suy ra \(BNMC\) là hình thang
b) Vì \(NM\) // \(BC\) (cmt)
Suy ra \(\widehat {{\rm{NMB}}} = \widehat {{\rm{MBC}}}\) (so le trong)
Mà \(\widehat {{\rm{MBN}}} = \widehat {{\rm{MBC}}}\) (do \(MB\) là phân giác)
Suy ra \(\widehat {{\rm{MBN}}} = \widehat {{\rm{NMB}}}\)
Suy ra \(\Delta MNB\) cân tại \(N\)
Suy ra \(BN = NM\)

a) Ta có : Vì góc BNA là góc ngoài của tam giác NAC nên
\(\widehat{BNA}=\widehat{C}+\widehat{NAC}=\widehat{C}+\frac{1}{2}\widehat{A}\)
Lại có
\(\hept{\begin{cases}\widehat{HAC}+\widehat{BAH}=90^0\\\widehat{HAC}+\widehat{HCA}=90^0\end{cases}\Rightarrow}\widehat{C}=\widehat{BAH}\)
Vậy \(\widehat{BAN}=\frac{1}{2}\widehat{A}+\widehat{C}=\widehat{BNA}\)hay tam giác BAN cân
b) K là giao của hai tia phân giác trong tam giác BAH nên BK cũng là phân giác của góc ABH
Mặt khác BM là đường trung tuyến trong tam giác cân BAN nên BM cũng là phân giác của góc ABN(\(\widehat{ABH}=\widehat{ABN}\))
Mà góc ABH chỉ có duy nhất 1 tia phân giác nên BK và BM trung nhau hay B,K,M thẳng hàng

a: BC=căn 9^2+12^2=15cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=15/7
=>BD=45/7cm; CD=60/7cm
AH=9*12/15=108/15=7,2cm
b: Xét ΔHAC vuông tại H và ΔMEA vuông tại M có
góc HCA=góc MAE
=>ΔHAC đồng dạng với ΔMEA
a, Góc C + góc KBC = 90 độ, góc C + HAC=90 độ nên góc HBP= góc NAH
HBP+HPB=90 độ, HPB=APQ (đối đỉnh) nên NAH+APQ=90 độ nên AN vuông góc với BQ
b, Tam giác APQ có đường cao cũng là đường phân giác nên tamg giác PAQ cân do đó AN cũng là đường trung trục của tam giác APQ, nên MP=MQ, tương tự sẽ có NP=MP=NP=MQ
do đó MPNQ là hình vuông
Ai tick cho phan hong phuc mà điểm tăng nhanh quá zậy