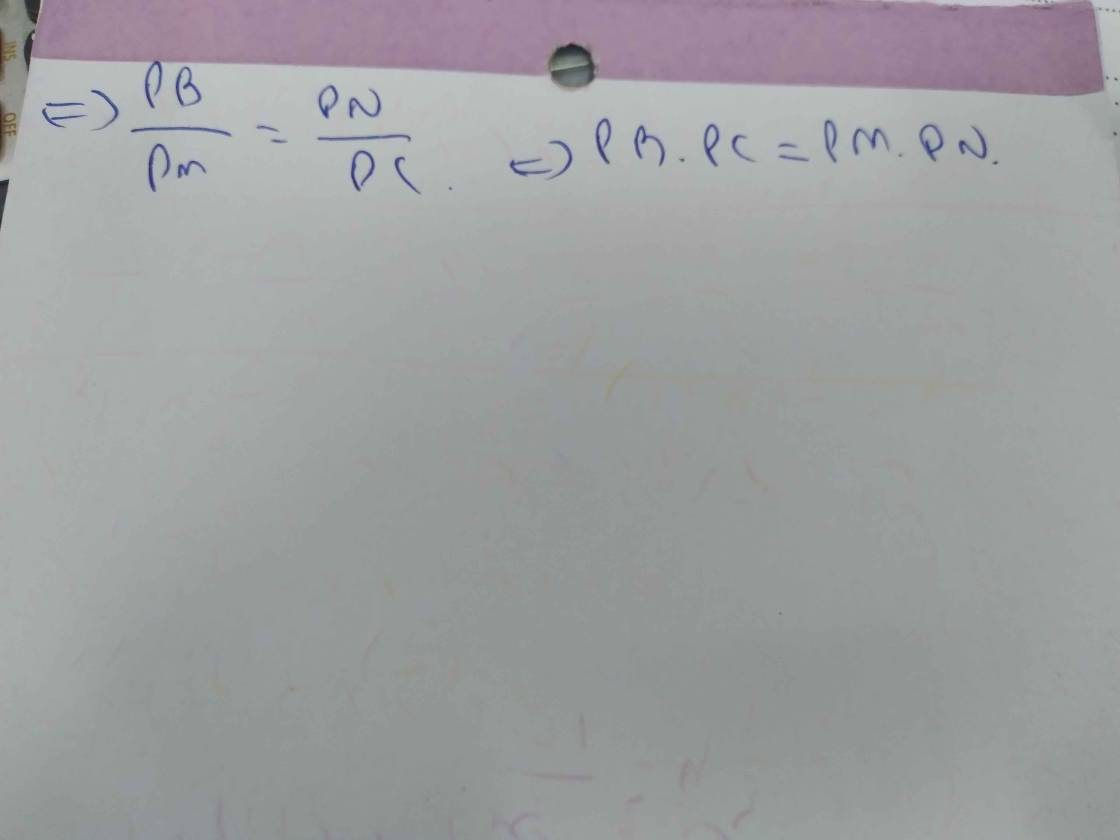Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

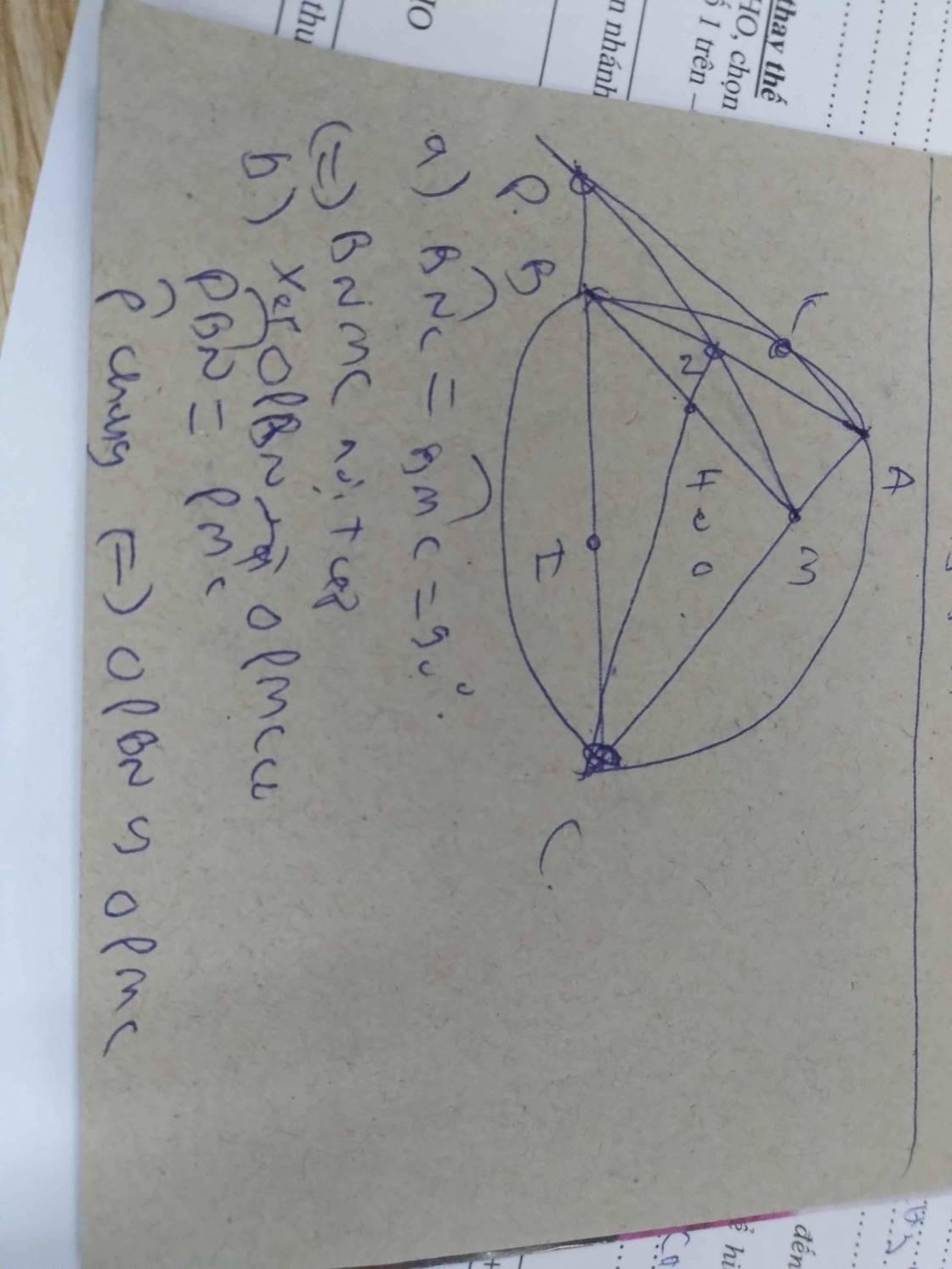
1: Xét tứ giác BCDE có \(\widehat{BDC}=\widehat{BEC}=90^0\)
nên BCDE là tứ giác nội tiếp
2: Xét ΔKEB vuông tại E và ΔKDC vuông tại D có
góc EKB=góc DKC
Do đó: ΔEKB\(\sim\)ΔDKC
Suy ra: KE/KD=KB/KC
hay \(KE\cdot KC=KB\cdot KD\)

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: Xet ΔBDH vuông tại D và ΔBEC vuông tại E có
góc DBH chung
=>ΔBDH đồng dạng với ΔBEC
=>BH/BC=DH/EC
=>BH*EC=DH*BC

a: Xét tứ giác BCDE có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BCDE là tứ giác nội tiếp
b: Xét ΔDHC vuông tại D và ΔDAB vuông tại D có
\(\widehat{HCD}=\widehat{ABD}\)
Do đó: ΔDHC\(\sim\)ΔDAB
Suy ra: DH/DA=DC/DB
hay \(DH\cdot DB=DA\cdot DC\)

tứ giác BFEC có hai góc kề nhau cùng nhìn đoạn BC dưới một góc vuông : BFCˆ=BECˆ(=90)BFC^=BEC^(=90) ==> Tức giác BFEC là tứ giác nội tiếp
==> 4 điểm B,E,F,C cùng thuộc một đường tròn.

a: góc OAD+góc OMD=180 độ
=>OADM nội tiếp
b: ΔOBC cân tại O
mà ON là đường cao
nên ONlà trung trực của BC
=>sđ cung NB=sd cung NC
=>góc BAN=góc CAN
=>AN là phân giác của góc BAC
góc DAI=1/2*sđ cung AN
góc DIA=1/2(sđ cung AB+sđ cung NC)
=1/2(sđ cung AB+sđ cung NB)
=1/2*sđ cung AN
=>góc DAI=góc DIA
=>ΔDAI cân tại D

3:
Xét ΔGMB và ΔGCA có
góc GMB=góc GCA
góc G chung
=>ΔGMB đồng dạng với ΔGCA
=>GM/GC=GB/GA
=>GM*GA=GB*GC
Xét ΔGEB và ΔGCD có
góc GEB=góc GCD
góc EGB chung
=>ΔGEB đồng dạng với ΔGCD
=>GE/GC=GB/GD
=>GE*GD=GB*GC=GM*GA
=>GE/GA=GM/GD
=>ΔGEM đồng dạng với ΔGAD
=>góc GEM=góc GAD
=>góc DEM+góc DAM=180 độ
=>ADEM nội tiếp
=>góc MDE=góc MAE